Question

How do you graph the equation $3y - 2x = 6$ on the coordinate plane ?

Answer 1

Hint: We have given an equation of a line as $3y - 2x = 6$ , which is a straight-line equation. A straight-line equation is always linear and represented as $y = mx + c$ where $m$ is the slope of the line and $c$ is the y-intercept and $\dfrac{{ - c}}{m}$ is the x-intercept .

Complete step by step solution:
We have equation of line,
 $
  3y - 2x = 6 \\
  or \\
  y = \dfrac{2}{3}x + \dfrac{6}{3} \\
   \Rightarrow y = \dfrac{2}{3}x + 2 \\
 $
Now we compare this given equation with the general linear equation i.e., $y = mx + c$
Hence ,
Slope of the given line, $m = \dfrac{2}{3}$ .
y-intercept of the given line , $c = 2$ .
Therefore, we can say that point $(0,2)$ lies on the line.
x-intercept of the given line , $\dfrac{{ - c}}{m} = \dfrac{{ - 2 \times 2}}{3} = \dfrac{{ - 4}}{3}$ .
Therefore, we can say that the point $(\dfrac{{ - 4}}{3},0)$ lies on the line.
With the help of two points, we can plot the graph by connecting the points as follow,

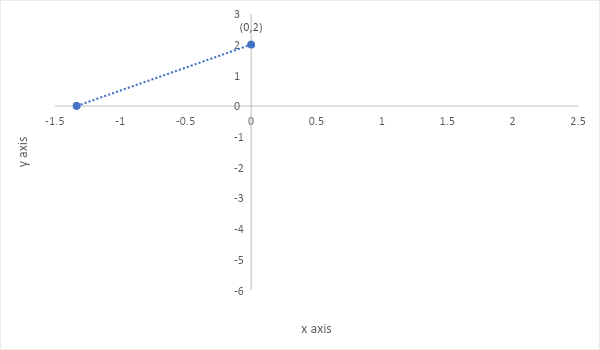
Note: This type of linear equations sometimes called slope-intercept form because we can easily find the slope and the intercept of the corresponding lines. This also allows us to graph it.
We can quickly tell the slope i.e., $m$ the y-intercepts i.e., $(y,0)$ and the x-intercept i.e., $(0,y)$ .we can graph the corresponding line .