Question

How do you graph the curve whose parametric equations are given and show its orientation given \[x = \sqrt t + 4\], \[y = \sqrt t - 4\], where \[t \geqslant 0\] ?

Answer 1

Hint:
Parametric equations are defined as, when a group of quantities of one or more independent variables formed as functions, then they are called parametric equations. For a parametric equation you put different values of t, where \[t \geqslant 0\], to get different pairs of values for x and y to get sets of points, joining which we get the desired curve.

Complete step by step solution:
Let us write the given equations as
\[x = \sqrt t + 4\] and
\[y = \sqrt t - 4\]
Let us consider t = 0, 1, 4, 9, 16, 25, 36 - note that we have intentionally selected square numbers, so that getting a pair of values of x and y is easy.
We get (4, −4), (5, −3), (6, −2), (7, −1), (8,0), (9,1), (10,2) and joining them we get the following graph and this is a straight line, shown below.

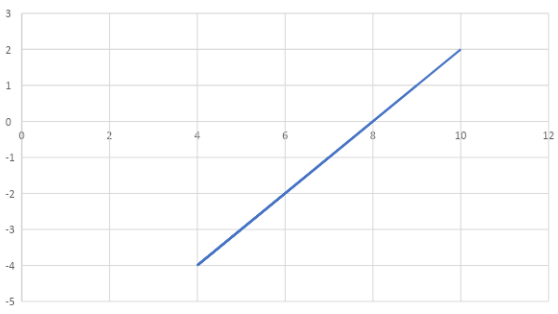
Also observe that given \[x = \sqrt t + 4\] and \[y = \sqrt t - 4\], subtracting from the former eliminates t and we get the equation of line \[x - y = 8\].

Here \[\sqrt t \] restricts line to \[x \geqslant 4\] or \[y \geqslant - 4\].

Additional information:
Parametric equations are used to represent the coordinates of a point for any geometrical object like curve, surfaces, etc., where the equations of these objects are said to be a parametric representation of that particular object.

Note:
Parametric functions are mainly used in the integration of different types of functions where the given function is in the complex form. In such cases, parameter t is used for substitution for some part of the given function. Other applications include graphs of various functions and equations that involve differentiation and so on.