
How do you graph the arithmetic sequence ${{a}_{n}}=2-\dfrac{1}{3}n$ ?
Answer
523.5k+ views
Hint: We have to first understand the meaning of a sequence that is an order of objects in line, where at every location, we get an object. We then have to draw an analogy between the behaviour of sequence and function and then replace n and ${{a}_{n}}$ in ${{a}_{n}}=2-\dfrac{1}{3}n$ with x and y respectively.
Complete step by step answer:
A sequence is an enumerated collection of objects, especially numbers, in which repetitions are allowed and in which the order of objects matters. A sequence may be finite or infinite depending on the number of objects in the sequence. Sequences can be of various types such as arithmetic sequence, geometric sequence and so on. Sequences can be completely random as well. The ${{n}^{th}}$ term of a sequence is sometimes written as a function of n.
In the problem, the ${{n}^{th}}$ term of the sequence is written as ${{a}_{n}}=2-\dfrac{1}{3}n$ which is a function of n. This means that as we change the value of n, the value of the corresponding term changes. There always exists a value of ${{a}_{n}}$ for any value of n. This reminds us of something. Similar behaviour is shown by a function $y=f\left( x \right)$ . In this function also, the value of changes for different values of x.
Thus, we can replace n and ${{a}_{n}}$ in ${{a}_{n}}=2-\dfrac{1}{3}n$ with x and y respectively. This then gives,
$\Rightarrow y=2-\dfrac{1}{3}x$
This is comparable to the slope-intercept form of a straight line $y=mx+c$ where m is the slope and c is the y-intercept. Upon comparing, $m=-\dfrac{1}{3},c=2$ . We can now draw the line.
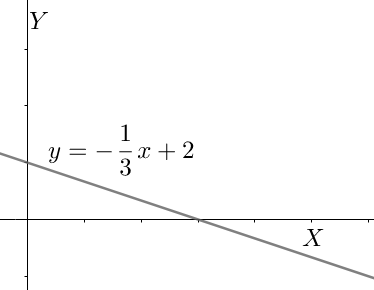
Note: These types of problems are tricky. Here, we have to assume that the sequence is infinite and then draw the analogy. We also need to correctly replace the notations to get the function and then correctly draw the graph.
Complete step by step answer:
A sequence is an enumerated collection of objects, especially numbers, in which repetitions are allowed and in which the order of objects matters. A sequence may be finite or infinite depending on the number of objects in the sequence. Sequences can be of various types such as arithmetic sequence, geometric sequence and so on. Sequences can be completely random as well. The ${{n}^{th}}$ term of a sequence is sometimes written as a function of n.
In the problem, the ${{n}^{th}}$ term of the sequence is written as ${{a}_{n}}=2-\dfrac{1}{3}n$ which is a function of n. This means that as we change the value of n, the value of the corresponding term changes. There always exists a value of ${{a}_{n}}$ for any value of n. This reminds us of something. Similar behaviour is shown by a function $y=f\left( x \right)$ . In this function also, the value of changes for different values of x.
Thus, we can replace n and ${{a}_{n}}$ in ${{a}_{n}}=2-\dfrac{1}{3}n$ with x and y respectively. This then gives,
$\Rightarrow y=2-\dfrac{1}{3}x$
This is comparable to the slope-intercept form of a straight line $y=mx+c$ where m is the slope and c is the y-intercept. Upon comparing, $m=-\dfrac{1}{3},c=2$ . We can now draw the line.
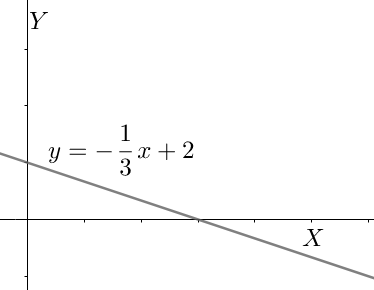
Note: These types of problems are tricky. Here, we have to assume that the sequence is infinite and then draw the analogy. We also need to correctly replace the notations to get the function and then correctly draw the graph.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the full form of pH?





