Question

How do you graph ${{r}^{2}}=\sin \left( 2\theta \right)$?

Answer 1

Hint: We can use the trigonometric identity $\sin \left( 2\theta \right)=2\sin \theta \cos \theta $ so that we can write the given equation as ${{r}^{2}}=2\sin \theta \cos \theta $. Then by using the relations ${{r}^{2}}={{x}^{2}}+{{y}^{2}}$, $x=r\cos \theta $ and $y=r\sin \theta $ we can convert the given equation to the Cartesian equation. Then by replacing $y$ by $x$ and vice-versa, we can check the symmetry about the line $y=x$. Then by substituting $y=0$ we can find out the intersection of the curve with the coordinate axes. Finally, we can equate the lowest degree term of the Cartesian equation to zero so as to get the tangents at the origin. With the help of these points, we can graph the given equation.

Complete step-by-step solution:
The equation given in the above question is written as
$\Rightarrow {{r}^{2}}=\sin \left( 2\theta \right)$
We know that $\sin \left( 2\theta \right)=2\sin \theta \cos \theta $. Therefore, the above equation can be written as
$\Rightarrow {{r}^{2}}=2\sin \theta \cos \theta $
Multiplying both sides by ${{r}^{2}}$ we get
$\begin{align}
  & \Rightarrow {{r}^{4}}=2{{r}^{2}}\sin \theta \cos \theta \\
 & \Rightarrow {{r}^{4}}=2\left( r\sin \theta \right)\left( r\cos \theta \right).......\left( i \right) \\
\end{align}$
Since the above equation is in the terms of the polar coordinates $r$ and $\theta $, it is a polar equation. We can convert it to the Cartesian equation by
$\begin{align}
  & \Rightarrow {{r}^{2}}={{x}^{2}}+{{y}^{2}}........\left( ii \right) \\
 & \Rightarrow x=r\cos \theta ..........\left( iii \right) \\
 & \Rightarrow y=r\sin \theta ..........\left( iv \right) \\
\end{align}$
Substituting the above equations (ii), (iii) and (iv) into the equation (i) we get
$\begin{align}
  & \Rightarrow {{\left( {{x}^{2}}+{{y}^{2}} \right)}^{2}}=2yx \\
 & \Rightarrow {{x}^{4}}+2{{x}^{2}}{{y}^{2}}+{{y}^{4}}=2xy \\
 & \Rightarrow {{x}^{4}}+2{{x}^{2}}{{y}^{2}}+{{y}^{4}}-2xy=0......\left( v \right) \\
\end{align}$
Now, we observe the above equation with respect to the below points
(i) Symmetry: Replacing $y$ by $x$ and $x$ by $y$ in the equation (v), we get
$\Rightarrow {{y}^{4}}+2{{y}^{2}}{{x}^{2}}+{{x}^{4}}-2yx=0$
The above equation is similar to the equation (v). Therefore, we can say that the curve will be symmetric with respect to the line $y=x$.
(ii) Intersection with Coordinate axes:
Substituting $x=0$ in (v) we get
$\begin{align}
  & \Rightarrow {{\left( 0 \right)}^{4}}+2{{\left( 0 \right)}^{2}}{{y}^{2}}+{{y}^{4}}-2\left( 0 \right)y=0 \\
 & \Rightarrow {{y}^{4}}=0 \\
 & \Rightarrow y=0 \\
\end{align}$
Since on substituting $x=0$, $y=0$ is obtained, the curve passes through the origin.
(iii) Tangent at the origin:
In the equation (v) we can observe that the lowest degree term is $-2xy$. Equating it to zero, we get
$\begin{align}
  & \Rightarrow 2xy=0 \\
 & \Rightarrow x=0,y=0 \\
\end{align}$
Therefore, the tangents at the origin are the x and the y axis.
Therefore, the curve can be sketched as

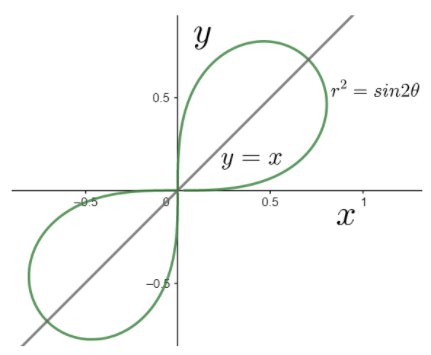
Hence, we have graphed ${{r}^{2}}=\sin \left( 2\theta \right)$.

Note: After changing the polar equation to the Cartesian equation, its sketching becomes easy. But we can sketch it without converting into the Cartesian equation too. For example, we can replace $\theta $ by $-\theta $ to check the symmetry about the initial line, and $r$ by $-r$ to check the symmetry about the pole.