Question

How do you graph $r = 1 - \sin \left( \theta \right)$ ?

Answer 1

Hint:The given expression is $r = 1 - \sin \left( \theta \right)$ which produces a cardioid. In the given expression $r = 1 - \sin \left( \theta \right)$ try to substitute different values for $\theta $ and find the corresponding values of $r$ and plot the graph for the same values.

Complete step by step answer:
The given expression that is $r = 1 - \sin \left( \theta \right)$ which is a polar coordinate produces the cardioid. Cardioid is nothing but a curve or a graph that somewhat looks like a heart-shaped curve.
The graph of a cardioid looks as shown below.

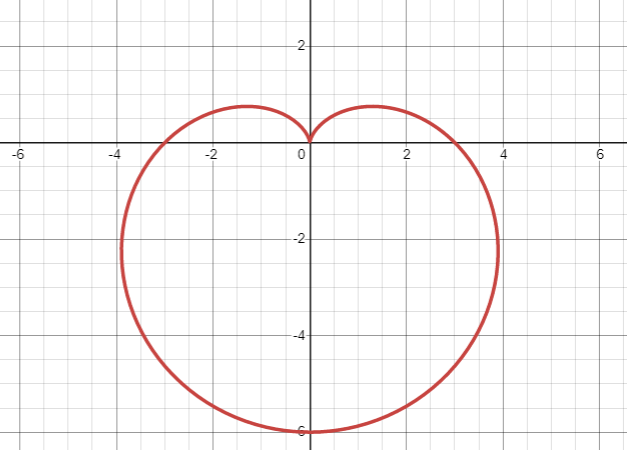
Now, to draw a graph for $r = 1 - \sin \left( \theta \right)$ , try to substitute different values for $\theta $ which varies from $0$ to $2\pi $.
The below table gives us the values of sine function for different values:
$\begin{array}{*{20}{c}}
  \theta &{{0^ \circ }}&{{{30}^ \circ }}&{{{45}^ \circ }}&{{{60}^ \circ }}&{{{90}^ \circ }}&{{{180}^ \circ }}&{{{270}^ \circ }}&{{{360}^ \circ }} \\
  {\sin \theta }&0&{\dfrac{1}{2}}&{\dfrac{{\sqrt 2 }}{2}}&{\dfrac{1}{2}}&1&0&{ - 1}&0
\end{array}$
Now we consider different values for $\theta $ to which we need to find the corresponding values of $r$ .
So let $\theta = 0$ now to find the corresponding value of $r$ we can write as below,
$ \Rightarrow r = 1 - \sin \left( {{0^ \circ }} \right) = 1 - 0 = 1$
At $\theta = {30^ \circ }$ the value of $r$ is
$ \Rightarrow r = 1 - \sin \left( {{{30}^ \circ }} \right) = 1 - \dfrac{1}{2} = \dfrac{1}{2}$
At $\theta = {60^ \circ }$ the value of $r$ is
$ \Rightarrow r = 1 - \sin \left( {{{30}^ \circ }} \right) = 1 - \dfrac{1}{2} = \dfrac{1}{2}$
At $\theta = {90^ \circ }$ the value of $r$ we get as
$ \Rightarrow r = 1 - \sin \left( {{{90}^ \circ }} \right) = 1 - 1 = 0$
In the same way the values of $r$ can be listed as below for different values of $\theta $ .
\[\begin{array}{*{20}{c}}
  \theta &{{0^ \circ }}&{{{30}^ \circ }}&{{{60}^ \circ }}&{{{90}^ \circ }}&{{{180}^ \circ }}&{{{270}^ \circ }}&{{{360}^ \circ }} \\
  r&1&{\dfrac{1}{2}}&{\dfrac{1}{2}}&0&1&2&1
\end{array}\]
Now, plot the graph for the above values. Which is shown as in the below figure.

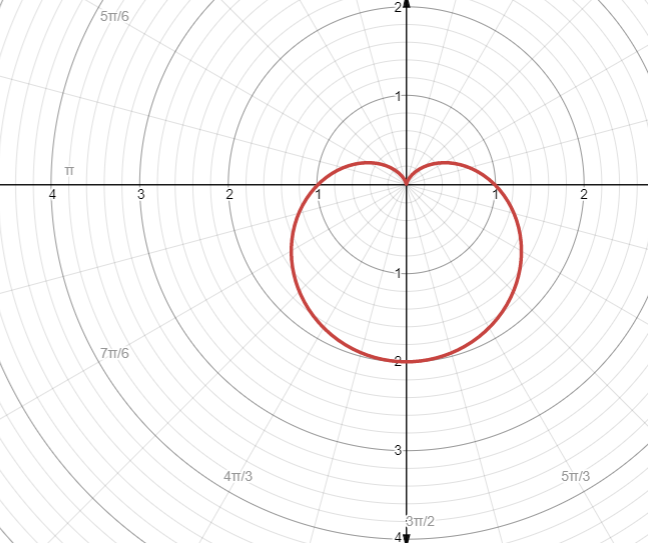
Therefore, the graph for the given expression $r = 1 - \sin \left( \theta \right)$ is as shown in the above figure.

Note: Whenever they ask us to draw a graph by giving an equation, then just take some values for one unknown that is for $\theta $ in the given equation and find the corresponding values of another unknown that is $r$ in this problem. Plot the same on a graph sheet as we did above.