Question

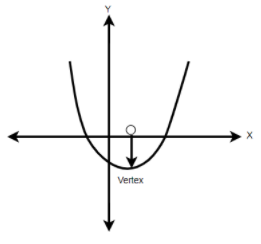
Graph of $y = a{x^2} + bx + c = 0$ is given. What conclusions can be drawn from this graph?

$\left( A \right){\text{ a > 0}}$
$\left( B \right){\text{ b < 0}}$
$\left( C \right){\text{ c < 0}}$
$\left( D \right){\text{ }}{{\text{b}}^2} - 4ac > 0$

Answer 1

Hint:
So in this question, we have a graph given and we have to do it. As we can see the curve and it is of the parabola and by using the properties of the parabola and its equation, we can answer these questions easily.

Complete step by step solution:
As we can see from the graph we have a parabola curve and since it is opening in an upward direction. So we can say that $a > 0$ and
Hence, the option $\left( a \right)$ is correct.
Here, we can see that the vertex of the parabola is located in the fourth quadrant, therefore it will be
$ \Rightarrow \dfrac{{{b^2}}}{{2a}} > 0$
And on solving it we get
$ \Rightarrow b < 0$
Therefore, the option $\left( b \right)$ is also correct.
Since, at $x = 0$ , the $y$ intercept will be positive and from this, we can conclude that $c < 0$ and Hence, the option $\left( c \right)$ will also be correct.
From the equation we can see that there are two real and distinct roots here, so from this, we can conclude that the $D > 0$ and it can also be written as ${b^2} - 4ac > 0$ .
Hence the last option is also correct.
On checking all the options, and we can see all options are correct and

Therefore, we conclude that all the options available are correct.

Note:
Here we can see that the graph was given to us and us to take out the conclusion from that since we have the options available so I would suggest you to always start to check from the options because by the use of options we can see how easily we concluded this question.