Question

How is the graph of $ - {\left( {x + 7} \right)^2} + 8 $ compared to the graph of $ f\left( x \right) = {x^2} $ ?

Answer 1

Hint: Here, we will consider the function $ f\left( x \right) = {x^2} $ as a parent function because we are asked to compare the given function with it. If we add signs and numbers around this parent function, another graph will look somewhat related to it with some changes. By these significant changes, we can compare any given graph with the main graph.

Complete step-by-step answer:
We are given the function $ - {\left( {x + 7} \right)^2} + 8 $ .
To answer our question, we will compare this function with the standard formula:
 $ a{(x + h)^2} + k $ Where,
The value of $ a $ stretch or compress the graph with respect to parent graph,
The value of $ h $ indicates the horizontal shift of the graph with respect to parent graph and
The value of $ k $ indicates the vertical shift of the graph with respect to the parent graph.
By comparing the given function $ - {\left( {x + 7} \right)^2} + 8 $ with $ a{(x + h)^2} + k $ , we get
 $ a = - 1 $ which indicates that the function is not stretched or compressed but only reflected with respect to the x axis.
 $ h = 7 $ which indicates that the graph shifts left to the parent graph by 7 units.
 $ k = 8 $ which indicates that the graph shifts up by 8 units with respect to the parent graph.
We can see these comparisons on the graph as:

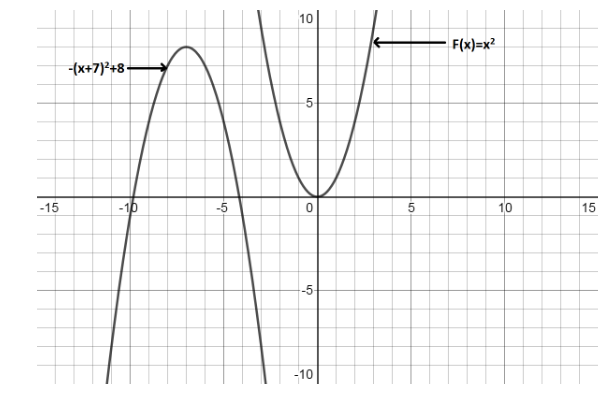
Note: In this problem, we have used the standard equation $ a{(x + h)^2} + k $ . Here, if the value of $ a $ is less than one, then the graph becomes narrower than the parent graph and it becomes wider if the value of $ a $ is greater than one. If the value of $ h $ is positive, the graph shifts left to the parent graph by $ h $ units and shifts right by $ h $ units if the value of $ h $ is negative. Finally, if the value of $ k $ is positive, the graph shifts up to the parent graph by $ k $ units and if it's negative then it will shift down by $ k $ units with respect to the parent unit.