Question

What is the graph of $f\left( x \right)={{x}^{\dfrac{2}{3}}}$?

Answer 1

Hint: To draw the graph of the function given in the above problem i.e. $f\left( x \right)={{x}^{\dfrac{2}{3}}}$, we can write this function as ${{\left( {{x}^{\dfrac{1}{3}}} \right)}^{2}}$. Now, we are going to draw the graph of ${{x}^{\dfrac{1}{3}}}$ then we will take the square of this function ${{x}^{\dfrac{1}{3}}}$.The changes which are observed when we square this function ${{x}^{\dfrac{1}{3}}}$are that: the part of the curve which lies in the negative y axis becomes positive by taking the mirror image of that part of the curve with x axis as the line mirror.

Complete step-by-step answer:
The function given in the above problem which we have to graph is as follows:
$f\left( x \right)={{x}^{\dfrac{2}{3}}}$
Now, to draw the graph of the above function, we can first of all going to rearrange the above function in the following way:
$f\left( x \right)={{\left( {{x}^{\dfrac{1}{3}}} \right)}^{2}}$
So, we are going to draw the graph of the above function by drawing the graph for ${{x}^{\dfrac{1}{3}}}$ first. Now, to draw the graph of ${{x}^{\dfrac{1}{3}}}$, we are going to equate this function to y and we get,
$y={{x}^{\dfrac{1}{3}}}$
Cubing on both the sides of the above equation we get,
${{y}^{3}}={{\left( {{x}^{\dfrac{1}{3}}} \right)}^{3}}$
The R.H.S of the above equation can be written in the following way:
${{y}^{3}}={{x}^{\dfrac{1}{3}\times 3}}$
In the exponent in the R.H.S of the above equation, 3 will get cancelled out from the numerator and the denominator and we get,
${{y}^{3}}=x$
To draw the graph of the above function, we are going to draw the graph of $y={{x}^{3}}$ which we know as follows:

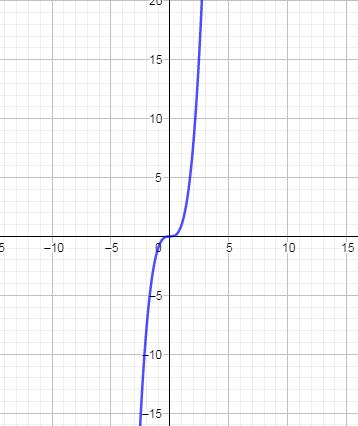
Now, the graph of ${{y}^{3}}=x$ is drawn in the same way which is drawn above but this graph will draw about x axis and it will look as follows:

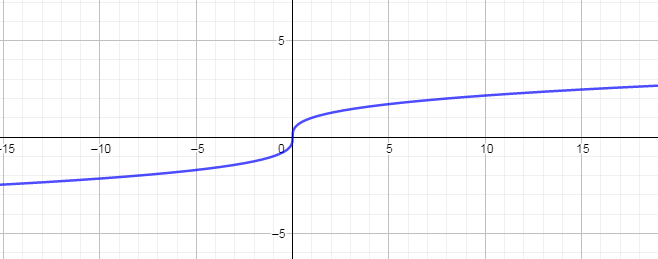
The above graph is the same as that of $y={{x}^{\dfrac{1}{3}}}$.
After the above drawing we are going to square the given function and the function will look as the original function given above:
$f\left( x \right)={{\left( {{x}^{\dfrac{1}{3}}} \right)}^{2}}$
Now, in the drawing of the above graph, as you can see that f(x) or y will take only positive values because the square of any number is always positive so we are going to take the mirror image of the negative y in the above figure and then remove that negative y part of the curve. Also, the other change which will observe is that all the y values gets increased by some factor but the profile remains same and the graph will look as follows:

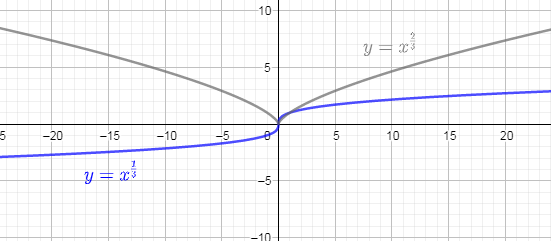
In the above graph, the curve drawn from the grey color is the graph of the function given in the above problem and blue curve is the curve of the function $y={{x}^{\dfrac{1}{3}}}$ which we have already shown.
Now, exclusively drawing the graph of the given function $f\left( x \right)={{x}^{\dfrac{2}{3}}}$ we get:

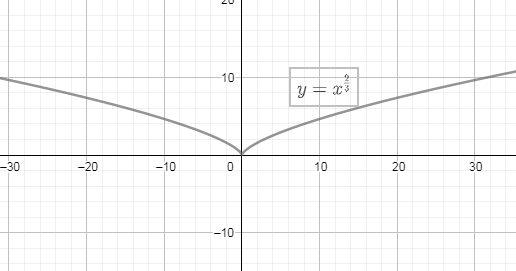
Hence, we have drawn the function given in the above problem.

Note: You will get the solution quickly if you do the above problem in the step wise manner otherwise it will be hard for you to draw the graph of the above function. The other way to draw the graph of the above function is to substitute different values of x starting from any negative value to the positive value and then plot them on the graph paper. There is nothing wrong in this approach but it will take a lot of time and this you cannot afford in the examination.