Question

How do you graph \[{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\]?

Answer 1

Hint: This is an equation of the circle is where on a plane the center is located. The equation of a circle is written as \[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\]. The \[h\] and \[k\] represent the coordinates of the center of the circle being at the point \[\left( {h,k} \right)\] and \[r\] represents the radius, the using the equation and substituting the \[h\], \[k\] and \[r\] values then we can plot the required graph.

Complete step-by-step solution:
Given an equation is an equation of the circle, In order to graph the equation of a circle is where on a plane the center is located. The equation of a circle is \[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\]. This is called the center-radius form (or standard form) because it gives you both pieces of information at the same time. The \[h\] and \[k\] represent the coordinates of the center of the circle being at the point \[\left( {h,k} \right)\] and \[r\] represents the radius.
Now the given equation is \[{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\], the equation is rewritten as
$ \Rightarrow {\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = {3^2}$
which is the equation of the circle, which is in form of \[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\], use this form to determine the center and radius of the circle.
Equate the values in this circle to those of the standard form. The variable \[r\] represents the radius of the circle, \[h\] represents the x-offset from the origin, and \[k\] represents the y-offset from the origin.
Here \[h = - 1,k = - 2\] and \[r = 3\],
The center of the circle is \[\left( {h,k} \right)\], so the center of the given circle is $\left( { - 1, - 2} \right)$, and the radius is 3.
Now plot the graph of the circle with the given data,

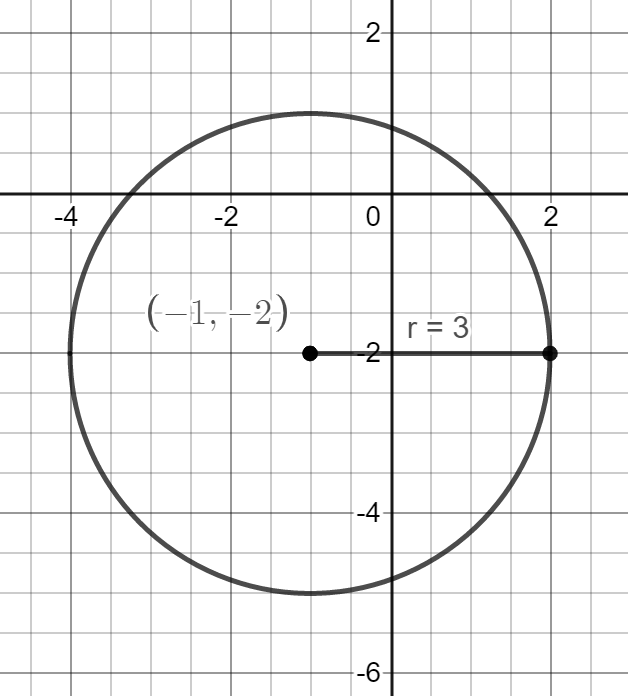
Note: We must know that the coordinates of the center of the circle are of the opposite signs of the \[h\] and \[k\] from inside the parentheses in the equation. Because the \[h\] and \[k\] are inside the grouping symbols, this means that the shift happens opposite from what we would think.