Question

How do you graph \[\left( \dfrac{{{x}^{2}}}{4} \right)-\left( \dfrac{{{y}^{2}}}{9} \right)=1\]?

Answer 1

Hint: We are asked to graph the given equation. Firstly, we deduce that the given equation is that of a hyperbola. Then, we will find the value of the center, foci, vertices, eccentricity and asymptotes using the given equation of the hyperbola. Then, using these obtained values, we will graph the given equation.

Complete step by step solution:
According to the given question, we are given an equation which we have to graph.
The equation we have is,
\[\left( \dfrac{{{x}^{2}}}{4} \right)-\left( \dfrac{{{y}^{2}}}{9} \right)=1\]-----(1)
We can see that the equation (1) is of the form \[\left( \dfrac{{{(x-h)}^{2}}}{{{a}^{2}}} \right)-\left( \dfrac{{{(y-k)}^{2}}}{{{b}^{2}}} \right)=1\]
which is the equation of a Hyperbola.
where \[(h,k)\] is the center of the hyperbola
So, in order to graph the given equation, we will have to find the center, vertices, foci, etc.
On comparing the equation (1) with the standard equation of the hyperbola, we get,
\[{{a}^{2}}=4\]
\[\Rightarrow a=2\]
\[{{b}^{2}}=9\]
\[\Rightarrow b=3\]
\[h=0\]
\[k=0\]
The center we have is \[(h,k)=(0,0)\].
Next, we have to find the vertex of the hyperbola. We know that the vertices can be found by adding ‘a’ to ‘h’ and the next one by subtracting ’a’ from ‘h’. We have,
\[(h+a,k)=(0+2,0)=(2,0)\]
\[(h-a,k)=(0-2,0)=(-2,0)\]
So, the vertices we have is, \[(2,0)\] and \[(-2,0)\].
Next, we will find the foci of the hyperbola, which is of the form, \[(h\pm \sqrt{{{a}^{2}}+{{b}^{2}}},k)\].
We will first find the value of \[\sqrt{{{a}^{2}}+{{b}^{2}}}\], we have,
\[\sqrt{{{a}^{2}}+{{b}^{2}}}=\sqrt{{{2}^{2}}+{{3}^{2}}}=\sqrt{4+9}=\sqrt{13}\]
The points of foci we have is,
\[(h+\sqrt{{{a}^{2}}+{{b}^{2}}},k)=(0+\sqrt{13},0)=(\sqrt{13},0)\]
\[(h-\sqrt{{{a}^{2}}+{{b}^{2}}},k)=(0-\sqrt{13},0)=(-\sqrt{13},0)\]
The foci we have are, \[(\sqrt{13},0)\] and \[(-\sqrt{13},0)\].
We will now also find the eccentricity of the hyperbola.
Eccentricity refers to the deviation in the usual property or norm.
It is given by the formula, \[\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{a}\].
Now, we will substitute the values in the equation and we get,
\[\Rightarrow \dfrac{\sqrt{{{2}^{2}}+{{3}^{2}}}}{2}=\dfrac{\sqrt{13}}{2}\]
So, the eccentricity is \[\dfrac{\sqrt{13}}{2}\].
Next, we will be finding the asymptotes.
An asymptote is a line which is tangent to a given curve and approaches as close as possible but does not touches that curve.
The formula for the asymptote is, \[y=\pm \dfrac{b(x-h)}{a}+k\]
Substituting the values in the above formula, we get the value of asymptote as,
\[\Rightarrow y=\pm \dfrac{3(x-0)}{2}+0\]
Solving further, we have,
\[\Rightarrow y=\pm \dfrac{3x}{2}\]
That is, the given hyperbola has two asymptotes which are: \[y=\dfrac{3x}{2}\] and \[y=-\dfrac{3x}{2}\].
The graph of the given equation using the points obtained, we have,

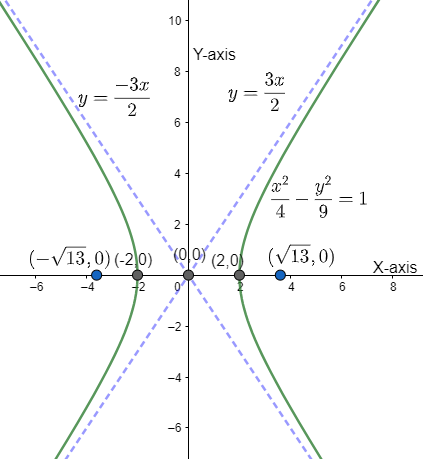
Note: The equation of hyperbola and the equation of ellipse is almost similar except for one difference and that is the negative sign in the equation, that is,
The equation of hyperbola is: \[\left( \dfrac{{{(x-h)}^{2}}}{{{a}^{2}}} \right)-\left( \dfrac{{{(y-k)}^{2}}}{{{b}^{2}}} \right)=1\]
The equation of ellipse is: \[\left( \dfrac{{{(x-h)}^{2}}}{{{a}^{2}}} \right)+\left( \dfrac{{{(y-k)}^{2}}}{{{b}^{2}}} \right)=1\]
So, while making the graph this point should be made clear and only then the other values are to be determined.