Question

How do you graph \[\left( {\dfrac{{{x^2}}}{4}} \right) - \left( {\dfrac{{{y^2}}}{9}} \right) = 1\]?

Answer 1

Hint:We use the definition of hyperbola and write its general equation. Compare the given equation to the general equation of hyperbola and write values of center and vertices.
* General equation of hyperbola having center \[(h,k)\]and vertices \[(h, \pm a)\]is given by the equation \[\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} - \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1\].

Complete step-by-step answer:
We are given the equation \[\left( {\dfrac{{{x^2}}}{4}} \right) - \left( {\dfrac{{{y^2}}}{9}} \right) = 1\]
We can write this equation in simpler form i.e. \[\dfrac{{{{\left( {x - 0} \right)}^2}}}{{{2^2}}} - \dfrac{{{{\left( {y - 0} \right)}^2}}}{{{3^2}}} = 1\]
On comparing this equation with general equation of hyperbola \[\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} - \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1\], we get
\[h = 0;k = 0\]
So, the center \[(h,k)\] of the parabola becomes \[(0,0)\] … (1)
Now from comparison we can also write \[a = 2;b = 3\]
So, the vertices \[(h, \pm a)\] of the hyperbola become \[(0, \pm 2)\]
Asymptotes are the straight lines that continuously approach the curve but never meet the curve
Now we can construct the hyperbola \[\left( {\dfrac{{{x^2}}}{4}} \right) - \left( {\dfrac{{{y^2}}}{9}} \right) = 1\] using its center \[(0,0)\] and its vertices \[(0, \pm 2)\]
We know the hyperbola will open in left and right side as the positive value of ‘x’
We first mark the center of hyperbola on the graph and then take 2 units in upward, downward, left and right direction

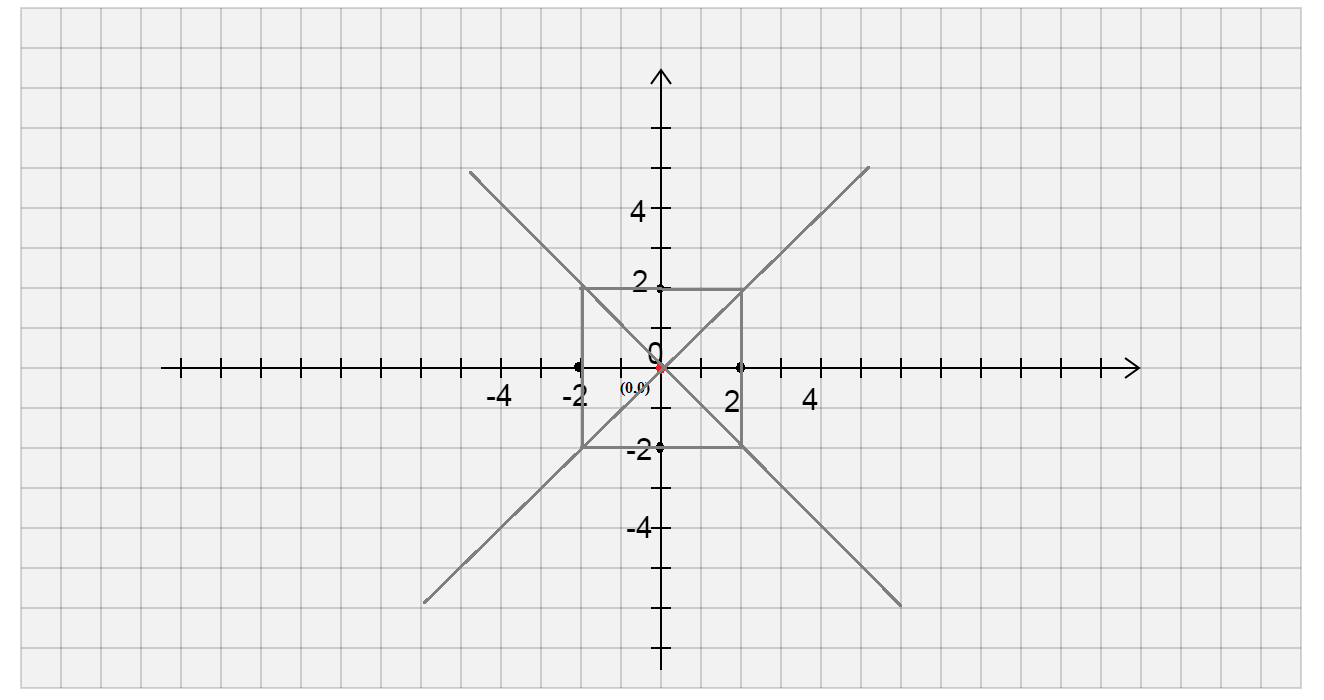
Now connect these corners as a rectangle and draw lines through corners as asymptotes

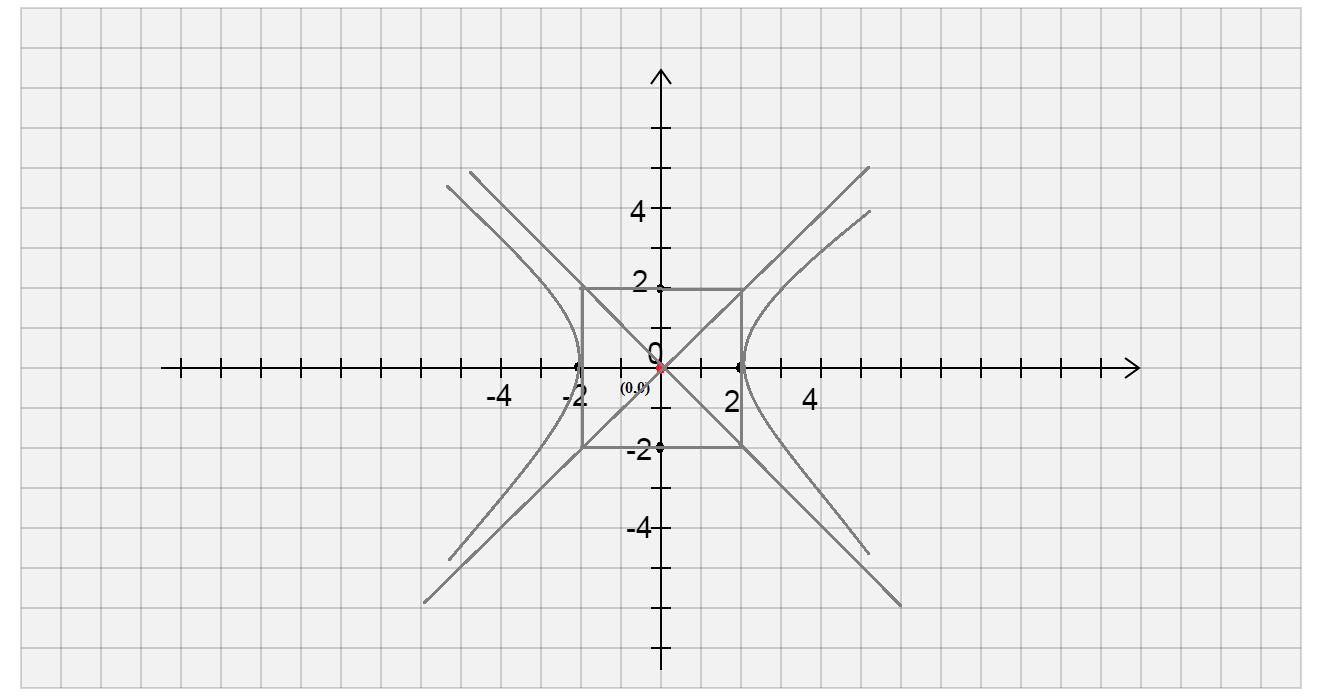
Draw hyperbola using the asymptotes opened on right and left side

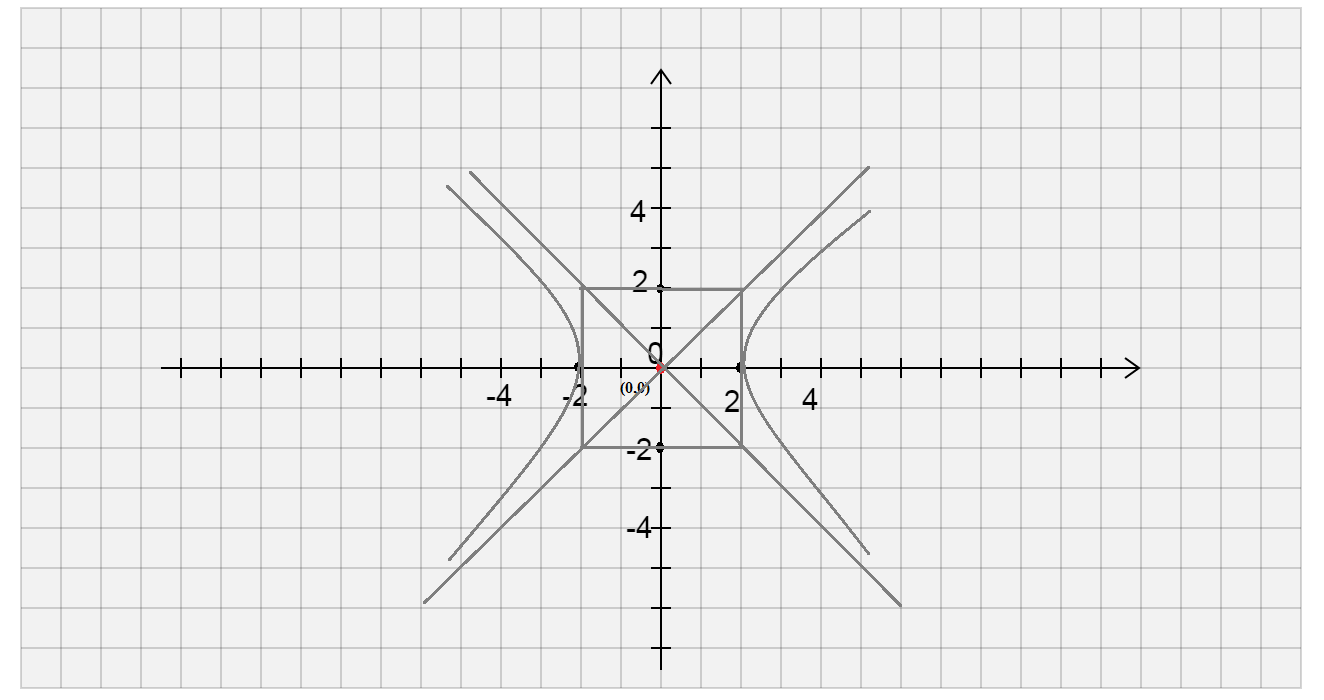
\[\therefore \]Graph of hyperbola \[\left( {\dfrac{{{x^2}}}{4}} \right) - \left( {\dfrac{{{y^2}}}{9}} \right) = 1\] is

Note:
Many students make mistake of assuming the equation given in the question as equation of an ellipse as they think the general equation of ellipse is \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] and they think negative sign just indicates graph is elliptical in which direction, but this is wrong concept. Keep in mind we never have a negative sign in an ellipse, a negative sign in such an equation tells us that the equation is of hyperbola.