Question

How do you graph $f\left( x \right)={{\left( x-2 \right)}^{2}}-1$ on a coordinate graph? \[\]

Answer 1

Hint: We recall that all quadratic polynomial $a{{x}^{2}}+bx+c\left( a\ne 0 \right)$ is a parabola opens upward which in vertex form can be written as $y={{\left( a-h \right)}^{2}}+k$ where vertex is $\left( h,k \right)$. We find the vertex and the point of intersection of $f\left( x \right)$ with $x-$axis from $f\left( x \right)=0$ and $y-$intercept from $f\left( 0 \right)$. We find one additional point on the curve and draw the parabola. \[\]

Complete step by step solution:
We know that if we plot any quadratic polynomial $a{{x}^{2}}+bx+c\left( a\ne 0 \right)$in coordinate graph we shall get a parabola opens upwards if $a > 0$ and opened downwards if $a < 0$. The equation of parabola opened either upward or downward with vertex $\left( h,k \right)$is given by
\[y=a{{\left( x-h \right)}^{2}}+k\]
We are given the following quadratic polynomial in the question
\[f\left( x \right)={{\left( x-2 \right)}^{2}}-1\]
We compare the above polynomial with $y=a{{\left( x-h \right)}^{2}}+k$ to have $y=f\left( x \right),a=1$ and vertex $\left( h,k \right)=\left( 2,-1 \right)$. So we shall get opened upward parabola since we have $a=1>0$. Let us find $x-$intercepts of the parabola as the zeroes of $f\left( x \right)$. We have
\[\begin{align}
  & f\left( x \right)=0 \\
 & \Rightarrow {{\left( x-2 \right)}^{2}}-1=0 \\
 & \Rightarrow {{\left( x-2 \right)}^{2}}-{{1}^{2}}=0 \\
\end{align}\]
We shall solve the above quadratic equation by factorization. We use the algebraic identity ${{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)$ for $a=x-2,b=1$ in the above step to have;
\[\begin{align}
  & \Rightarrow \left\{ \left( x-2 \right)+1 \right\}\left\{ \left( x-2 \right)-1 \right\}=0 \\
 & \Rightarrow \left( x-1 \right)\left( x-3 \right)=0 \\
\end{align}\]
Since the product of two factors is zero then at least one of the factors is zero. So we have
\[\begin{align}
  & \Rightarrow x-1=0\text{ or }x-3=0 \\
 & \Rightarrow x=1\text{ or }x=3 \\
\end{align}\]
So we have two more points$\left( 1,0 \right),\left( 3,0 \right)$where graph of $f\left( x \right)$ cuts $x-$axis. Let us find the $y-$intercept at $x=0$. we have
\[f\left( 0 \right)={{\left( 0-2 \right)}^{2}}-1=4-1=3\]
So we have $\left( 0,3 \right)$ where graph of $f\left( x \right)$ cuts $y-$axis. Let us take another point $x=4$ and have
\[\begin{align}
  & f\left( 4 \right)={{\left( 4-2 \right)}^{2}}-1 \\
 & \Rightarrow f\left( 4 \right)={{2}^{2}}-1 \\
 & \Rightarrow f\left( 4 \right)=3 \\
\end{align}\]
So we have another point $\left( 4,3 \right)$. We use the obtained points $\left( 1,0 \right),\left( 3,0 \right),\left( 0,3 \right),\left( 4,3 \right)$ and draw the upward parabola at vertex $\left( 2,-1 \right)$\[\]
 

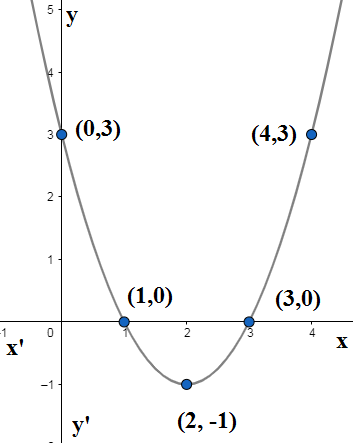
Note: We note that the other form upward parabola is $y=a{{x}^{2}}+bx+c\left( a > 0 \right)$ where the vertex can be obtained as $x=\dfrac{-b}{2a}$ and also there is another form ${{\left( x-h \right)}^{2}}=4a\left( y-k \right)$ where $2a$ is the length of latus rectum the longest chord of parabola. We note the minima of the quadratic polynomial occurs at vertex .