
How do you graph \[f\left( x \right)={{4}^{x}}+2\] by plotting points?
Answer
541.5k+ views
Hint: This question is from the topic of algebra. In this question, we will draw the graph of \[f\left( x \right)={{4}^{x}}+2\]. In solving this question, we will draw a table for about 11 values of x and using those values we will find the values of f(x). After using values of x and f(x), we will draw a graph putting the value of x along the x-axis and putting the values of f(x) along the y-axis.
Complete step-by-step answer:
Let us solve this question.
In this question, we have asked to draw the graph of given equation by plotting points. The given equation is
\[f\left( x \right)={{4}^{x}}+2\]
Let us put the values in place of x and find the values of x.
At x=-(infinity),
\[f\left( -\infty \right)={{4}^{-\infty }}+2\]
The above can also be written as
\[\Rightarrow f\left( -\infty \right)=\dfrac{1}{{{4}^{\infty }}}+2\]
As we know that \[{{x}^{\infty }}=\infty \], where \[x>1\]
So, we can write
\[\Rightarrow f\left( -\infty \right)=\dfrac{1}{\infty }+2\]
As we know that inverse of infinity is zero, so we can write the above as
\[\Rightarrow f\left( -\infty \right)=0+2=2\]
Let us check at x=-4, we can write
\[f\left( -4 \right)={{4}^{-4}}+2=0.003+2=2.003\]
Now, let us check at x=-3, we can write
\[f\left( -3 \right)={{4}^{-3}}+2=0.0156+2=2.0156\]
Now, let us check at x=-2, we can write
\[f\left( -2 \right)={{4}^{-2}}+2=0.0625+2=2.0625\]
Now, let us check at x=-1, we can write
\[f\left( -1 \right)={{4}^{-1}}+2=0.25+2=2.25\]
Now, let us check at x=0, we can write
\[f\left( 0 \right)={{4}^{0}}+2=1+2=3\]
Now, let us check at x=1, we can write
\[f\left( 1 \right)={{4}^{1}}+2=4+2=6\]
Let us check at x=2, we can write
\[f\left( 2 \right)={{4}^{2}}+2=16+2=18\]
Now, let us check at x=infinity, we can write
\[f\left( \infty \right)={{4}^{\infty }}+2\]
As we know that \[{{x}^{\infty }}=\infty \], where \[x>1\], so we can write
\[\Rightarrow f\left( \infty \right)=\infty +2\]
As infinity is largest number, so if we add any number with infinity, it will be infinity.
\[\Rightarrow f\left( \infty \right)=\infty \]
Now, we will draw the on the above values that we have taken and found.
Now, we will draw the graph using this table, where we will take x along x-axis and take \[f\left( x \right)\] along y-axis.
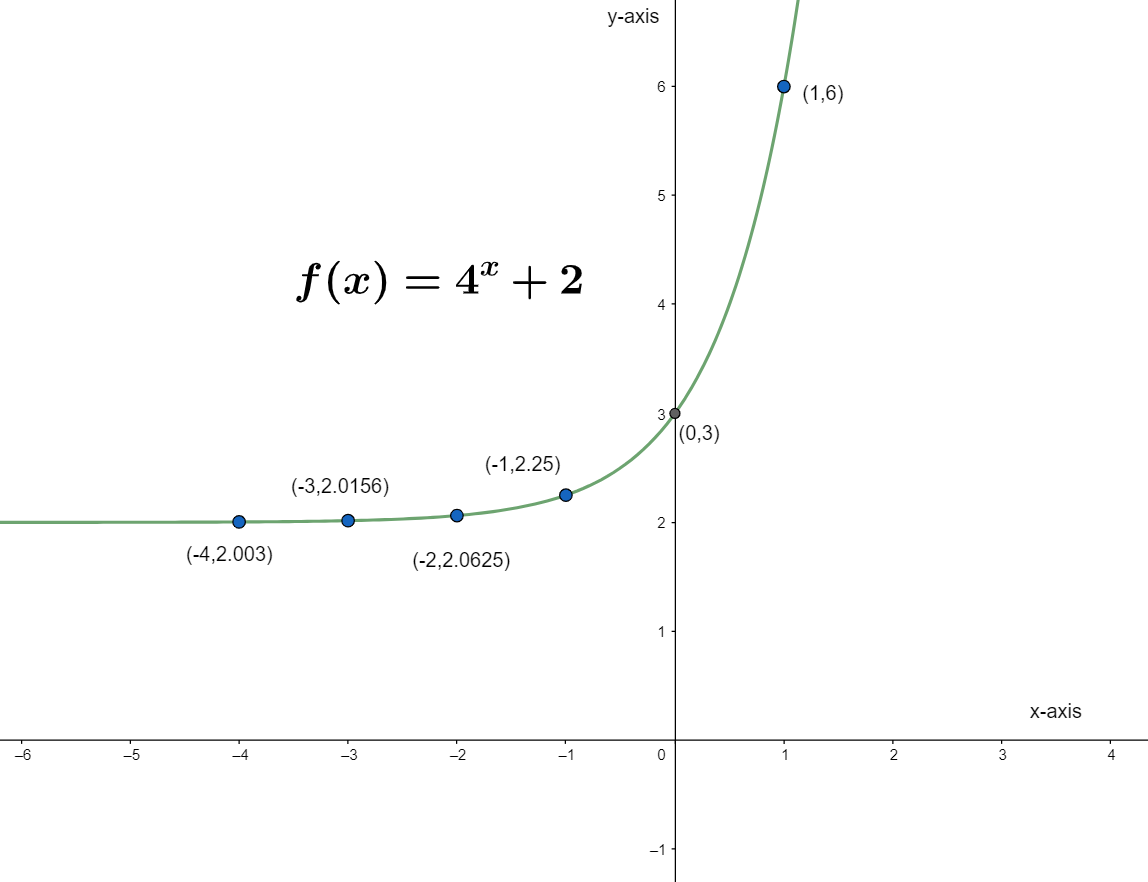
Here, we can see that at x=-(infinity), the graph is at y=2 and at x=infinity, the graph is going to infinity.
Hence, now we have drawn the graph of \[f\left( x \right)={{4}^{x}}+2\] by plotting the points.
Note: As we can see that this question is from the topic of algebra, so we should have a better knowledge in that topic. We should know how to draw the graph of any equation by plotting the points.
Remember that:
\[{{x}^{\infty }}=\infty \], where \[x>1\]
\[{{x}^{-\infty }}=0\], where \[x<1\]
\[\dfrac{1}{\infty }=0\]
Complete step-by-step answer:
Let us solve this question.
In this question, we have asked to draw the graph of given equation by plotting points. The given equation is
\[f\left( x \right)={{4}^{x}}+2\]
Let us put the values in place of x and find the values of x.
At x=-(infinity),
\[f\left( -\infty \right)={{4}^{-\infty }}+2\]
The above can also be written as
\[\Rightarrow f\left( -\infty \right)=\dfrac{1}{{{4}^{\infty }}}+2\]
As we know that \[{{x}^{\infty }}=\infty \], where \[x>1\]
So, we can write
\[\Rightarrow f\left( -\infty \right)=\dfrac{1}{\infty }+2\]
As we know that inverse of infinity is zero, so we can write the above as
\[\Rightarrow f\left( -\infty \right)=0+2=2\]
Let us check at x=-4, we can write
\[f\left( -4 \right)={{4}^{-4}}+2=0.003+2=2.003\]
Now, let us check at x=-3, we can write
\[f\left( -3 \right)={{4}^{-3}}+2=0.0156+2=2.0156\]
Now, let us check at x=-2, we can write
\[f\left( -2 \right)={{4}^{-2}}+2=0.0625+2=2.0625\]
Now, let us check at x=-1, we can write
\[f\left( -1 \right)={{4}^{-1}}+2=0.25+2=2.25\]
Now, let us check at x=0, we can write
\[f\left( 0 \right)={{4}^{0}}+2=1+2=3\]
Now, let us check at x=1, we can write
\[f\left( 1 \right)={{4}^{1}}+2=4+2=6\]
Let us check at x=2, we can write
\[f\left( 2 \right)={{4}^{2}}+2=16+2=18\]
Now, let us check at x=infinity, we can write
\[f\left( \infty \right)={{4}^{\infty }}+2\]
As we know that \[{{x}^{\infty }}=\infty \], where \[x>1\], so we can write
\[\Rightarrow f\left( \infty \right)=\infty +2\]
As infinity is largest number, so if we add any number with infinity, it will be infinity.
\[\Rightarrow f\left( \infty \right)=\infty \]
Now, we will draw the on the above values that we have taken and found.
| \[x\] | \[-\infty \] | -4 | -3 | -2 | -1 | 0 | 1 | 2 | \[\infty \] |
| \[f\left( x \right)\] | 2 | 2.003 | 2.0156 | 2.0625 | 2.25 | 3 | 6 | 18 | \[\infty \] |
Now, we will draw the graph using this table, where we will take x along x-axis and take \[f\left( x \right)\] along y-axis.

Here, we can see that at x=-(infinity), the graph is at y=2 and at x=infinity, the graph is going to infinity.
Hence, now we have drawn the graph of \[f\left( x \right)={{4}^{x}}+2\] by plotting the points.
Note: As we can see that this question is from the topic of algebra, so we should have a better knowledge in that topic. We should know how to draw the graph of any equation by plotting the points.
Remember that:
\[{{x}^{\infty }}=\infty \], where \[x>1\]
\[{{x}^{-\infty }}=0\], where \[x<1\]
\[\dfrac{1}{\infty }=0\]
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




