
Graph $f\left( x \right) = {x^4} - 3{x^2} + 2x$
Answer
546.9k+ views
Hint: Given a polynomial and we have to plot a graph of the polynomial. To plot the graph of the polynomial, first, we will factorize the equation. Then set each factor equal to zero to find the x and y intercepts of the equation. Then the set of these values can be plotted on the set of axes. Then we will join the points to obtain the graph of the polynomial.
Complete step by step answer:
We are given the polynomial $f\left( x \right) = {x^4} - 3{x^2} + 2x$. Compute the value of $y$-intercept by substituting $x = 0$ into the equation.
$f\left( 0 \right) = {0^4} - 3{\left( 0 \right)^2} + 2\left( 0 \right)$
On simplifying the equation, we get:
$ \Rightarrow f\left( 0 \right) = 0$
Now we will find the $x$-intercept by substituting $y = 0$ into the equation.
${x^4} - 3{x^2} + 2x = 0$
Take out the common term of the expression.
$ \Rightarrow x\left( {{x^3} - 3x + 2} \right) = 0$
Now, we will find the factor of the expression using the factor theorem. So, substitute $x = 1$into the expression.
$ \Rightarrow {\left( 1 \right)^3} - 3\left( 1 \right) + 2 = 1 - 3 + 2$
On simplifying the equation, we get:
$ \Rightarrow 1 - 3 + 2 = 0$
Thus, $x = 1$ is a root of the polynomial. Therefore, $\left( {x - 1} \right)$ is a factor of the equation. Now, apply the long division method to find the quadratic equation.
\[
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline {{\text{ }}{x^2} + x - 2{\text{ }}} \\
x - 1){x^3} + 0{x^2} - 3x + 2 \\
\,\,\,\,\,\,\,\,\,\,\underline {( - ){x^3} - {x^2}{\text{ }}} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x^2} - 3x \\
\,\,\,\,\,\,\,\,\,\,\underline {( - ){x^2} - x{\text{ }}} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,- 2x + 2 \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline { - 2x + 2} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \\ \]
Thus, the factors of the polynomial are $x\left( {x - 1} \right)\left( {{x^2} + x - 2} \right) = 0$
Now, further factorize the expression by splitting the middle term whose sum is $1$ and product is $ - 2$.
$ \Rightarrow x\left( {x - 1} \right)\left( {{x^2} + 2x - x - 2} \right) = 0$
$ \Rightarrow x\left( {x - 1} \right)\left[ {x\left( {x + 2} \right) - 1\left( {x + 2} \right)} \right] = 0$
$ \Rightarrow x\left( {x - 1} \right)\left( {x - 1} \right)\left( {x + 2} \right) = 0$
Now, set each factor equal to zero to find the $x$-intercepts.
$ \Rightarrow x = 0{\text{ or }}x - 1 = 0{\text{ or }}x + 2 = 0$
$ \Rightarrow x = 0{\text{ or }}x = 1{\text{ or }}x = - 2$
Now, write the intercepts of the polynomial in the form of ordered pairs.
$\left( {0,0} \right)$, $\left( {1,0} \right)$ and $\left( { - 2,0} \right)$
Now we will plot the points on the set of $x$-axis and $y$-axis. Then join these points to obtain the graph of the polynomial.
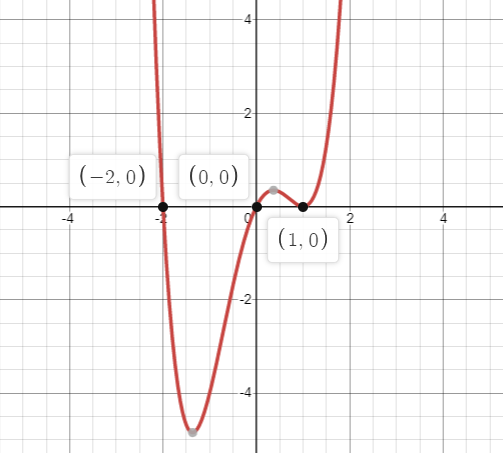
Final answer: Hence the graph of the polynomial is
Note: In such types of questions students mainly do mistakes while plotting the points on the set of axes. In an ordered pair$\left( {x,y} \right)$, the value of $x$ is the distance of the point from $y$-axis whereas the value of $y$ is plotted by taking the distance from the $x$-axis. In such types of questions, the graph of a polynomial is obtained by plotting these points and must be in a straight line.
Complete step by step answer:
We are given the polynomial $f\left( x \right) = {x^4} - 3{x^2} + 2x$. Compute the value of $y$-intercept by substituting $x = 0$ into the equation.
$f\left( 0 \right) = {0^4} - 3{\left( 0 \right)^2} + 2\left( 0 \right)$
On simplifying the equation, we get:
$ \Rightarrow f\left( 0 \right) = 0$
Now we will find the $x$-intercept by substituting $y = 0$ into the equation.
${x^4} - 3{x^2} + 2x = 0$
Take out the common term of the expression.
$ \Rightarrow x\left( {{x^3} - 3x + 2} \right) = 0$
Now, we will find the factor of the expression using the factor theorem. So, substitute $x = 1$into the expression.
$ \Rightarrow {\left( 1 \right)^3} - 3\left( 1 \right) + 2 = 1 - 3 + 2$
On simplifying the equation, we get:
$ \Rightarrow 1 - 3 + 2 = 0$
Thus, $x = 1$ is a root of the polynomial. Therefore, $\left( {x - 1} \right)$ is a factor of the equation. Now, apply the long division method to find the quadratic equation.
\[
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline {{\text{ }}{x^2} + x - 2{\text{ }}} \\
x - 1){x^3} + 0{x^2} - 3x + 2 \\
\,\,\,\,\,\,\,\,\,\,\underline {( - ){x^3} - {x^2}{\text{ }}} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x^2} - 3x \\
\,\,\,\,\,\,\,\,\,\,\underline {( - ){x^2} - x{\text{ }}} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,- 2x + 2 \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline { - 2x + 2} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \\ \]
Thus, the factors of the polynomial are $x\left( {x - 1} \right)\left( {{x^2} + x - 2} \right) = 0$
Now, further factorize the expression by splitting the middle term whose sum is $1$ and product is $ - 2$.
$ \Rightarrow x\left( {x - 1} \right)\left( {{x^2} + 2x - x - 2} \right) = 0$
$ \Rightarrow x\left( {x - 1} \right)\left[ {x\left( {x + 2} \right) - 1\left( {x + 2} \right)} \right] = 0$
$ \Rightarrow x\left( {x - 1} \right)\left( {x - 1} \right)\left( {x + 2} \right) = 0$
Now, set each factor equal to zero to find the $x$-intercepts.
$ \Rightarrow x = 0{\text{ or }}x - 1 = 0{\text{ or }}x + 2 = 0$
$ \Rightarrow x = 0{\text{ or }}x = 1{\text{ or }}x = - 2$
Now, write the intercepts of the polynomial in the form of ordered pairs.
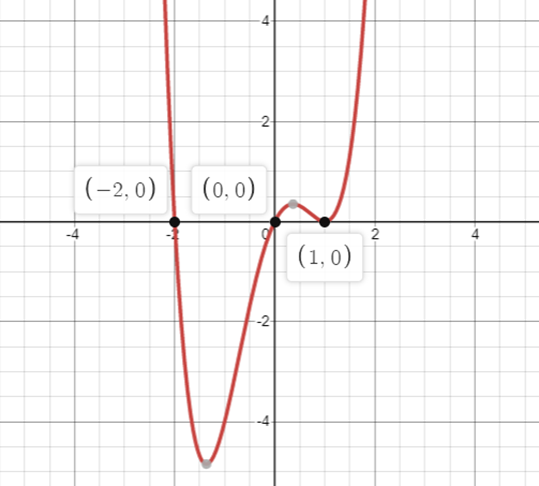
$\left( {0,0} \right)$, $\left( {1,0} \right)$ and $\left( { - 2,0} \right)$
Now we will plot the points on the set of $x$-axis and $y$-axis. Then join these points to obtain the graph of the polynomial.

Final answer: Hence the graph of the polynomial is

Note: In such types of questions students mainly do mistakes while plotting the points on the set of axes. In an ordered pair$\left( {x,y} \right)$, the value of $x$ is the distance of the point from $y$-axis whereas the value of $y$ is plotted by taking the distance from the $x$-axis. In such types of questions, the graph of a polynomial is obtained by plotting these points and must be in a straight line.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

What is a periderm How does periderm formation take class 11 biology CBSE

What are porins class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Differentiate between red algae and brown algae class 11 biology CBSE

What is boron A Nonmetal B Metal C Metalloid D All class 11 chemistry CBSE




