Question

How do you graph and determine if $y = {\left( {\dfrac{4}{3}} \right)^x}$ is a growth or decay?

Answer 1

Hint: In the function $y = {\left( {\dfrac{4}{3}} \right)^x}$, base is greater than 1 (as $\dfrac{4}{3} > 1$). So this becomes the graph of exponential function $y = {a^x}$ where $a > 1$.Refer to the standard graph of ${a^x}$ graph for $a > 1$. This is also an increasing function because if we increase the power of any number which is greater than 1, its value increases. It is also a property of $y = {a^x}$ when $a > 1$.

Complete step-by-step solution:
According to the question, we have to draw the graph of a function and determine whether it’s a growth or decay.
The given function is:
$ \Rightarrow y = {\left( {\dfrac{4}{3}} \right)^x}$
This is an exponential function and its base is $\dfrac{4}{3}$ which is greater than 1. So we can compare this function with the standard exponential function $y = {a^x}$ when $a > 1$.
We already know the graph of the function $y = {a^x}$ for both the cases, when $a > 1$ and when $a < 1$. This is shown below:

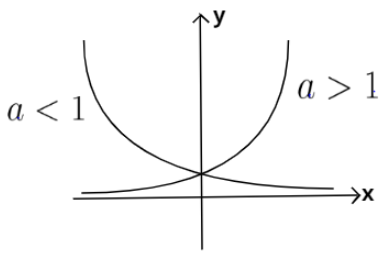
From this, we will only consider the graph of the function where $a > 1$ because the base of our function is greater than 1.
Thus the graph of the function $y = {\left( {\dfrac{4}{3}} \right)^x}$ is as shown below:

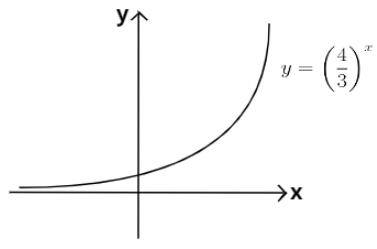
Also this function will be an increasing function because we know that as we increase the power of a number which is greater than 1, its value increases. This is also evident from the graph of the function as the value of $y$ is increasing when the value of $x$ is increasing. Hence this is a growth.

Note: (1) When the base of such function is less than 1 i.e. $y = {a^x}$ when $a < 1$, then such a function will always be a decay or decreasing function because we already know that when we increase the raised power of a number which is less than, its value decreases. This graph is also shown below.

(2) If we replace $a$ in the function $y = {a^x}$ by $e$, this will become $y = {e^x}$ and its graph will be increasing because $e > 1$.