Question

How to graph a parabola $y = {x^2} - 4x - 5$?

Answer 1

Hint:In order graph the parabola to the above quadratic equation ,first identity the nature of roots of the equation by finding the value of determinant using formula $D = {b^2} - 4ac$.D>0 means the both the roots are distinct and real .
These roots are nothing but the points of x-intercept at which the parabola touches the x-axis. To determine the roots use the quadratic formula .
Then they find out the vertex by using x coordinate as$x = - \dfrac{b}{{2a}}$and at the end determine is there a y- intercept or not by putting $x = 0$in the equation. Graph all these coordinates to get your desired graph of the parabola.

Complete step by step solution:
We are given a quadratic equation $y = {x^2} - 4x - 5$
The equation is quadratic in terms of variable $x$,so the graph will be an Upward opening parabola.
Comparing the equation with the standard quadratic equation$a{x^2} + bx + c$,we get
$
a = 1 \\
b = - 4 \\
c = - 5 \\
$
To graph this quadratic, we have to first find the nature of roots of the equation .For this we will calculate the determinant(D)
$
D = {b^2} - 4ac \\
= {( - 4)^2} - 4(1)( - 5) \\
= 16 + 20 \\
= 36 \\
$
Since $D > 0$,the quadratic equation is having both roots as distinct real.
By this we can say that the graph of parabola will have two x-intercept .
For points of intercept ,we will find the solution to the quadratic equation. Let the roots of the equation be $x1\,and\,x2$
$
x1 = \dfrac{{ - b + \sqrt D }}{{2a}} \\
= \dfrac{{ - ( - 4) + \sqrt {36} }}{{2.(1)}} \\
= \dfrac{{4 + 6}}{{2.(1)}} \\
= \dfrac{{10}}{2} \\
= 5 \\
$
and
$
x2 = \dfrac{{ - b - \sqrt {{b^2} - 4ac} }}{{2a}} \\
= \dfrac{{ - ( - 4) - \sqrt {36} }}{{2.(1)}} \\
= \dfrac{{4 - 6}}{{2.(1)}} \\
= \dfrac{{ - 2}}{2} \\
= - 1 \\
$
Hence, the points $(0,5)$and $\left( {0, - 1} \right)$both the x-intercept of the graph
Now finding the x-coordinate of the vertex(V)
$
x = - \dfrac{b}{{2a}} \\
= - \dfrac{{( - 4)}}{{2.1}} \\
= \dfrac{4}{2} \\
= 2 \\
$
Now putting $x = 2$in the original equation to determine the y-coordinate of the vertex(V)
$
y = {2^2} - 4.2 - 5 \\
= 4 - 8 - 5 \\
= - 9 \\
$
Therefore the vertex of the parabola will be at $(2, - 9)$.
We can have a look at is there any y-intercept of the graph .So, to find this put$x = 0$into the equation, we get
$
y = {x^2} - 4x - 5 \\

= {0^2} - 4.0 - 5 \\
= - 5 \\
$
So, y-intercept also exists at $(0, - 5)$.
Therefore, the parabola to the equation $y = {x^2} - 4x - 5$will be,

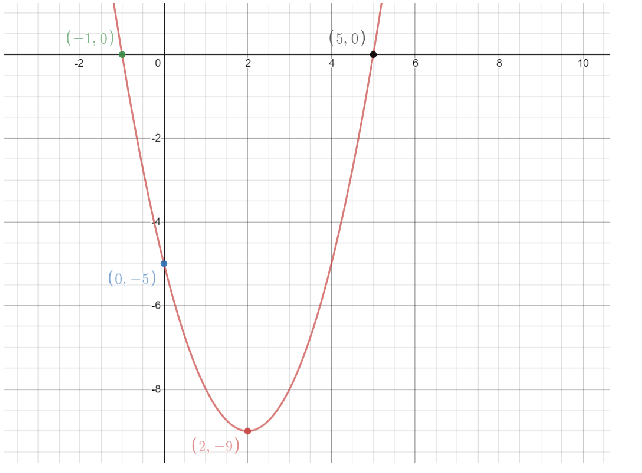
Hence, we have successfully plotted the parabola of the equation$y = {x^2} - 4x - 5$.

Alternative:
You can also alternatively use a direct method which uses Quadratic Formula to find both roots of a quadratic equation as

$x1 = \dfrac{{ - b + \sqrt {{b^2} - 4ac} }}{{2a}}$ and $x2 = \dfrac{{ - b - \sqrt {{b^2} - 4ac} }}{{2a}}$
x1,x2 are root to quadratic equation $a{x^2} + bx + c$

Hence the factors will be $(x - x1)\,and\,(x - x2)\,$.

Additional Information:
Quadratic Equation: A quadratic equation is a equation which can be represented in the form of $a{x^2} + bx + c$where $x$is the unknown variable and a,b,c are the numbers known where $a \ne 0$.If $a = 0$then the equation will become a linear equation and will no longer be quadratic .

The degree of the quadratic equation is of the order 2.

Every Quadratic equation has 2 roots.

Discriminant: $D = {b^2} - 4ac$

Using Discriminant, we can find out the nature of the roots
If D is equal to zero, then both of the roots will be the same and real.
If D is a positive number then, both of the roots are real solutions.
If D is a negative number, then the root are the pair of complex solutions

Note: 1. One must be careful while calculating the answer as calculation error may come.

2.Don’t forget to compare the given quadratic equation with the standard one every time.

3.Draw the cartesian plane only with the help of a straight ruler and pencil to get the perfect and accurate results.