Question

How do you graph \[5x+y=-5\] using intercepts?

Answer 1

Hint: We are asked to draw the graph of the equation \[5x+y=-5\]. The degree of an equation is the highest power of the variable present in it. So, for this equation, the highest power present \[x\] is 1, the degree is also 1. From this, it can be said that this is a linear equation. The graph of a linear equation represents a straight line.

Complete step by step answer:
The general equation of a straight line is \[ax+by+c=0\], where \[a,b,c\] are any real numbers. The given equation is \[5x+y=-5\], the equation can also be written as \[5x+y+5=0\], comparing with the general equation of straight line, we get \[a=5,b=1\And c=5\].
To plot the graph of an equation of the straight line, we should know at least two points, through which the line passes.
To make things simple, let’s take the X-intercept and Y-intercept as the two points. X-intercept is the point where the line crosses X-axis, this means that the Y-coordinate will be \[0\], similarly Y-intercept is the point where the line crosses Y-axis, so X-coordinate will be \[0\]. We will use this property now.
We substitute \[y=0\] in the equation \[5x+y+5=0\], we get
\[\begin{align}
  & \Rightarrow 5x+0+5=0 \\
 & \Rightarrow 5x+5=0 \\
\end{align}\]
Subtracting 5 from both sides of the equation we get,
\[\begin{align}
  & \Rightarrow 5x+5-5=0-5 \\
 & \Rightarrow 5x=-5 \\
\end{align}\]
We divide 5 to both sides we get,
\[\begin{align}
  & \Rightarrow \dfrac{5x}{5}=\dfrac{-5}{5} \\
 & \therefore x=-1 \\
\end{align}\]
So, the coordinates of the X-intercept are \[\left( -1,0 \right)\].
Similarly, now we substitute \[x=0\] in the equation, we get
\[\begin{align}
  & \Rightarrow 5(0)+y+5=0 \\
 & \Rightarrow y+5=0 \\
\end{align}\]
Subtracting 5 from both sides of the equation, we get
\[\begin{align}
  & \Rightarrow y+5-5=0-5 \\
 & \therefore y=-5 \\
\end{align}\]
So, the coordinates of the Y-intercept are \[\left( 0,-5 \right)\].
Using these two points we can plot the graph of the equation as follows:

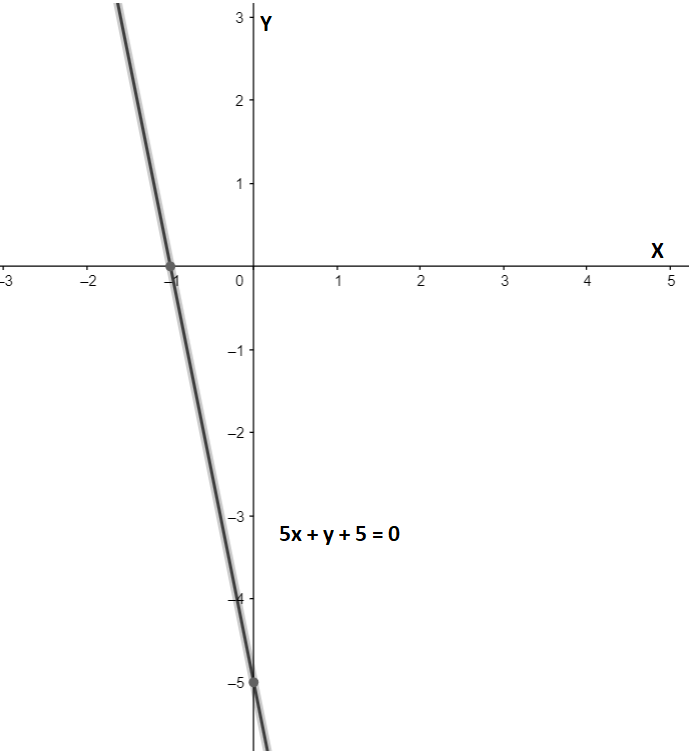
Note:
Here, we found the two points which are X-intercept and Y-intercept by substituting either x or \[y\] to be zero, one at a time. We can also find these values by converting the straight-line equation to the equation in intercept form which is, \[\dfrac{x}{a}+\dfrac{y}{b}=1\]. Here, \[a\And b\]are X-intercept and Y-intercept respectively.