Question

How do you graph \[3{x^2} + 3{y^2} - 6x + 12y = 0\] ?

Answer 1

Hint: Since, the given equation contains two variables with squared powers, it is the equation of a circle. The general equation of a circle having its center other than the origin is \[{(x - a)^2} + {(y - b)^2} = {r^2}\].

Complete Step by Step Solution:
First step is to make this equation in its simple form. This can be done by taking out \[3\] from the entire equation.
\[3{x^2} + 3{y^2} - 6x + 12y = 0\]
\[ \Rightarrow 3({x^2} + {y^2} - 2x + 4y) = 0\]
\[ \Rightarrow {x^2} + {y^2} - 2x + 4y = 0\]
Now, identify the geometrical figure, whose equation can be like this. It is known that in the equation of a circle, the two variables involved have squared powers. Hence, this equation is a circle. Now, remembering the standard equation of the circle, the following two equations come to mind.
\[1){x^2} + {y^2} = {r^2}\] This equation is followed when the center of the circle is at the origin. Here, \[r\]is the radius of the circle.
\[2){(x - a)^2} + {(y - b)^2} = {r^2}\]This equation is followed when the center of the circle is not at the origin. Here, \[r\]is the radius of the circle and \[(a,b)\] are the coordinates of the point which is the center of the circle.
The equation given in the question is definitely the expanded form of the type 2 equation mentioned above.
After realizing it to be the equation of a circle with type 2 form, we have to modify the given equation in such a form that it becomes exactly the same. This modification can be brought by the completing the squares method.
We are using the completing the squares method because the equation given in the question resembles the expanded form as \[{(x + a)^2} = {x^2} + {a^2} + 2ax\]
\[{x^2} + {y^2} - 2x + 4y = 0\]
According to\[{x^2} + {a^2} + 2ax\], the above equation lacks the constant term required for completing the square.
Rearranging we get
\[ \Rightarrow {x^2} - 2x + {y^2} + 4y = 0\]
We see that we are lacking constant terms, therefore, we add \[1\] and \[4\] on both sides of the equation, we get
\[ \Rightarrow {x^2} - 2x + {y^2} + 4y + 1 + 4 = 1 + 4\]
Rearranging we get
\[ \Rightarrow {x^2} - 2x + 1 + {y^2} + 4y + 4 = 5\]
Grouping together to form squares we get,
\[ \Rightarrow {({x^{}} - 1)^2} + {(y + 2)^2} = 5\]
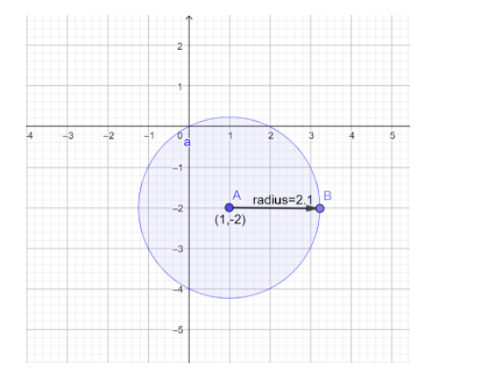
Hence, the desired form is obtained. From this form we are able to find the coordinates of the center and the length of radius which are \[(1, - 2)\]and\[\sqrt 5 \]
To find the intercepts, we just need to compare our equation with the standard equation \[{x^2} + {y^2} + 2gx + 2fy + c = 0\]
And from this we know that the formula of intercepts is X and Y intercepts as
\[2\sqrt {{g^2} - c} \] and \[2\sqrt {{f^2} - c} \]
In our equation,
\[g = - 1\]
\[f = 2\]
\[c = 0\]
Therefore, Y intercept is
\[2\sqrt {{g^2} - c} = 2\sqrt {{2^2} - 0} = 2 \times 2 = 4\]units
And, X intercept is
\[2\sqrt {{f^2} - c} = 2\sqrt {{1^2} - 0} = 2 \times 1 = 2\]units

Note: One should always remember the standard equations before approaching these types of problems.
Also, it is necessary to know the complete square method of solving quadratic equations. The most commonly used formula in this question was \[{(x + a)^2} = {x^2} + {a^2} + 2ax\]
A circle is a collection of points in a plane that are equidistant from a given fixed point.