Question

How do you graph \[3x + 4y = - 10\] using intercepts?

Answer 1

Hint: Intercepts of a graph are points at which the graph crosses the axes. To graph the equation using intercepts, we must find x and y intercepts. To find the x-intercept, set y = 0 and solve for x, to find the y-intercept, set x = 0 and solve for y, hence by solving we get the x and y intercepts and to graph a line, graph the points if they exist, and then connect the two points with a straight line.

Complete step-by-step answer:
Let us write the given linear equation:
  \[3x + 4y = - 10\]
To graph the solution for the given equation, we need to find x and y intercepts.
Let us find the x-intercepts: To find the x-intercept, set y = 0 and solve for x i.e.,
 \[3x + 4y = - 10\]
 \[3x + 4\left( 0 \right) = - 10\]
 \[ \Rightarrow \] \[3x = - 10\]
Divide both sides of the equation by 3 to get the value of x as
 \[\dfrac{{3x}}{3} = \dfrac{{ - 10}}{3}\]
We get the value of x as,
 \[ \Rightarrow \] \[x = \dfrac{{ - 10}}{3}\]
Hence, the x-intercept of the given equation is \[\left( { - \dfrac{{10}}{3},0} \right)\] .
Now let us find the y-intercepts: To find the y-intercept, set x = 0 and solve for y i.e.,
 \[3x + 4y = - 10\]
 \[3\left( 0 \right) + 4y = - 10\]
 \[4y = - 10\]
Divide both sides of the equation by 4 to get the value of y as
 \[\dfrac{{4y}}{4} = \dfrac{{ - 10}}{4}\]
 \[ \Rightarrow \] \[y = - \dfrac{{10}}{4}\]
The value of y is,
 \[y = - \dfrac{5}{2}\]
Hence, the y-intercept of the given equation is \[\left( {0, - \dfrac{5}{2}} \right)\] or \[\left( {0, - 2.5} \right)\]
Now, let us graph the solution: to graph this line using the intercepts, first graph the two points as shown A = \[\left( { - \dfrac{{10}}{3},0} \right)\] and B = \[\left( {0, - 2.5} \right)\] ,then connect the two points with a straight line.

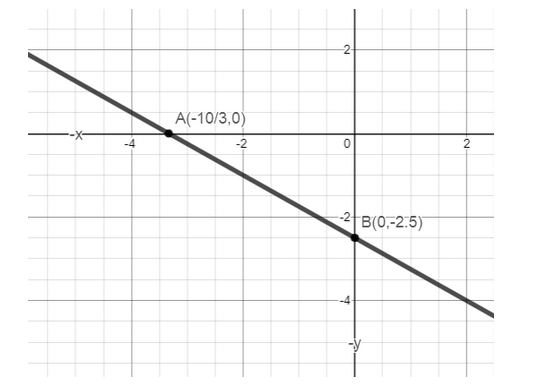
Note: We can then plot the two intercepts on the coordinate plane, and any line can be graphed using two points i.e., select two x values, and plug them into the equation to find the corresponding y values and we must know that the intercepts are deduced when x or y equals one and the x-intercepts occurs when y is zero and y-intercepts occurs when x is zero, hence this is the key point to note while solving for intercepts.