Question

How do you graph $2x-3y=9$ using x and y intercepts?

Answer 1

Hint:
The x-intercept is the point where the y coordinate of the point is equal to zero and y-intercept is the point where the x coordinate of the point is equal to zero. To find x intercept substitute $y=0$ and for the x- intercept substitute $x=0$ in the given equation.

Complete step by step solution:
They can write the given equation as $2x-3y-9=0$ …. (i)
We can see that the given equation is the general form of the equation of a straight line.
I.e. $ax+by+c=0$, where a, b and c are real numbers.
Therefore, we have confirmed that the given equation is an equation of a straight line.
The x-intercept of a line is the point where the straight line cuts or meets the x-axis and the y-intercept of a line is the point where the straight line cuts or meets the y-axis.
This means that x-intercept is the point where the y coordinate of the point is equal to zero and y-intercept is the point where the x coordinate of the point is equal to zero.
Therefore,
Substitute $x=0$ in equation (i).
Then,
$\Rightarrow 2(0)-3y-9=0$
$\Rightarrow y=-3$
This means that the y intercept for the given line is $(0,-3)$
Now, Substitute $y=0$ in equation (i).
Then,
$\Rightarrow 2x-3(0)-9=0$
$\Rightarrow x=\dfrac{9}{2}$
This means that the x intercept for the given line is $\left( \dfrac{9}{2},0 \right)$.
Now, plot the two points, $(0,-3)$ and $\left( \dfrac{9}{2},0 \right)$ on a Cartesian plane and draw the line that connects both the points.

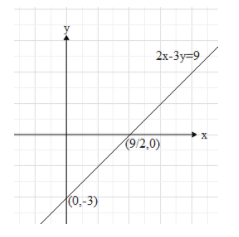
Note:
There is another method to find the x and y intercepts of a line and that is by writing the given equation of line in intercepts form.
The intercept form of line is given as $\dfrac{x}{a}+\dfrac{y}{b}=1$.
Where a and b are x and y intercepts respectively.