Question

How do you graph $2x+3y=3$ using intercepts?

Answer 1

Hint: In order to solve this question, we must have prior knowledge about intercepts of a straight-line and how they are represented in the equation of a line. We will find the x-intercept and y-intercept of the given equation of straight. Further, we will plot those on a graph and create the graph of the given function.

Complete step-by-step answer:
The x-intercept is the distance from origin of the point on the given function where the value of y is zero. This point logically lies on the x-axis and is given as $\left( a,0 \right)$ where $a$ is called the x-intercept.
The y-intercept is the distance from origin of the point on the given function where the value of x is zero. This point logically lies on the y-axis and is given as $\left( 0,b \right)$ where $b$ is called the y-intercept.
We are given the function, $2x+3y=3$.
In order to find the x-intercept, we will put $y=0$ and solve the equation accordingly. Hence, putting $y=0$, we get
$\begin{align}
  & \Rightarrow 2x+3\left( 0 \right)=3 \\
 & \Rightarrow 2x=3 \\
\end{align}$
Taking 2 on the right-hand side, we get
$\Rightarrow x=\dfrac{3}{2}$
Therefore, the x-intercept is equal to $\dfrac{3}{2}.$
In order to find the y-intercept, we will put $x=0$ and solve the equation accordingly. Hence, putting $x=0$, we get
$\begin{align}
  & \Rightarrow 2\left( 0 \right)+3y=3 \\
 & \Rightarrow 3y=3 \\
\end{align}$
Taking 3 on the right-hand side, we get
$\Rightarrow y=\dfrac{3}{3}$
$\Rightarrow y=1$
Therefore, the y-intercept is equal to $1.$
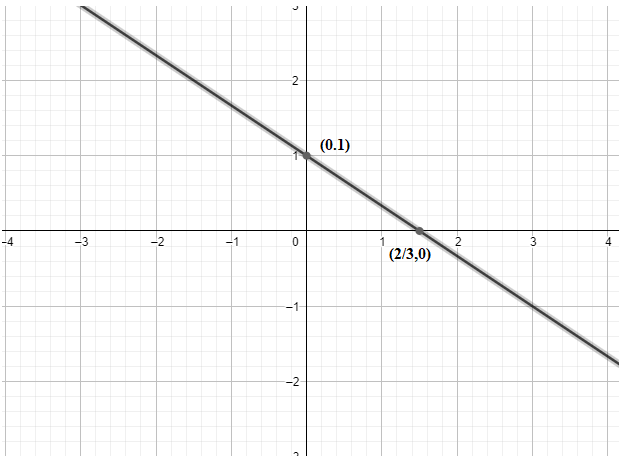
Hence, we get our two points as $\left( \dfrac{3}{2},0 \right)$ and $\left( 0,1 \right)$.
Therefore, we get our graph as:

Note:
The equation of a straight line is expressed especially in an intercept form which is given as $\dfrac{x}{a}+\dfrac{y}{b}=1$ where $a$ is the x-intercept of line and $b$ is the y-intercept of the line as mentioned before. One essential feature of the intercept form of line is that its constant term is always equal to 1.