Question

What is gradient and how can we find it?

Answer 1

Hint: It is to measure the steepness of a slope.
The steeper a slope is the higher the gradient.
The shallower the slope is the smaller the gradient.
First, we are going to consider a line on the graph and then we are going to consider a straight and on it there are two points, we are going to use these points and substitute them into the slope formula and the slope/ gradient of the line in the graph.

Complete step by step answer:
Gradient is another word for slope. Higher is the gradient of any graph at any point, steeper is the line at that point
Finding the gradient of a straight-line
The gradient of the line = (change in y-coordinate)/(change in x-coordinate)

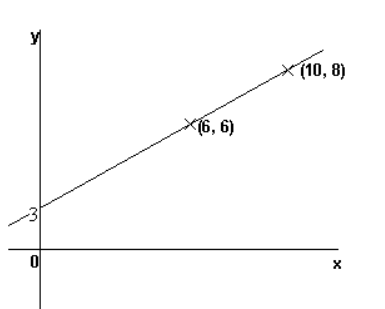
In this graph, the \[gradient{\text{ }} = \dfrac{{\left( {change{\text{ }}in{\text{ }}y - coordinate} \right)}}{{\left( {change{\text{ }}in{\text{ }}x - coordinate} \right)}} = \dfrac{{\left( {8 - 6} \right)}}{{\left( {10 - 6} \right)}}{\text{ }} = {\text{ }}\dfrac{2}{4}{\text{ }} = {\text{ }}\dfrac{1}{2}\]
Also, there is another formula for finding the slope between the two points$({x_1},{y_1}),({x_2},{y_2})$ of the same line, it is
$Slope = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \dfrac{{\left( {8 - 6} \right)}}{{\left( {10 - 6} \right)}}{\text{ }} = {\text{ }}\dfrac{2}{4}{\text{ }} = {\text{ }}\dfrac{1}{2}$
Similarly, we can find the slope of any given curve at a point by drawing a tangent from that point.
Since, we also have the slope of the line, we can even find the equation of the line by the general form $y = mx + c$, where we have the value of m which is slope and c is the constant which \[y = 3\] and on substituting we get
$y = \dfrac{1}{2}x + 3$
The above is the equation of the line whose slope or gradient is \[{\text{ }}\dfrac{1}{2}\].
We should also know that the gradient of two parallel lines is equal.

Note: The gradient of some line or curve shows us how much one variable differs in comparison to another variable.
Any system that changes will be described using rates of change that can be visualized as gradients of mathematical functions.
It can also be used by taking a dot product to calculate how a scalar field shifts in other ways, rather than just the direction of the greatest transit.