Question

Given\[n(A) = 285,n(B) = 195,n(U) = 500,n(A \cup B) = 410\], find \[n(A' \cup B')\]

Answer 1

Hint: Venn diagrams are used to represent the relation between the sets. Here, the number of sets A, B, and their union have been given and we need to find the union of its complementary sets. We will use the suitable formula of sets to find the unknown terms.

Formula: Some of the formulas we need to know:
1.\[n(A \cup B) = n(A) + n(B) - n(A \cap B)\]
2.\[n(A' \cup B') = n(A \cap B)' = n(U) - n(A \cap B)\]
Complete step by step answer:
It is given that \[n(A) = 285,n(B) = 195,n(U) = 500,n(A \cup B) = 410\]
We aim to find the value of the term \[n(A' \cup B')\]. We can use the formula \[n(A' \cup B') = n(A \cap B)' = n(U) - n(A \cap B)\] to find the value \[n(A' \cup B')\]. We have the value \[n(U)\]but we don’t know the value of \[n(A \cap B)\] we need to find that.
Let us consider the formula \[n(A \cup B) = n(A) + n(B) - n(A \cap B)\].
Let us draw the Venn diagram for a clear representation.
                                                                                   \[n(A \cup B)\]

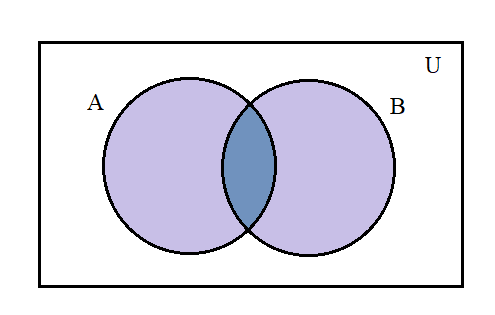
                                                 \[n(A)\]

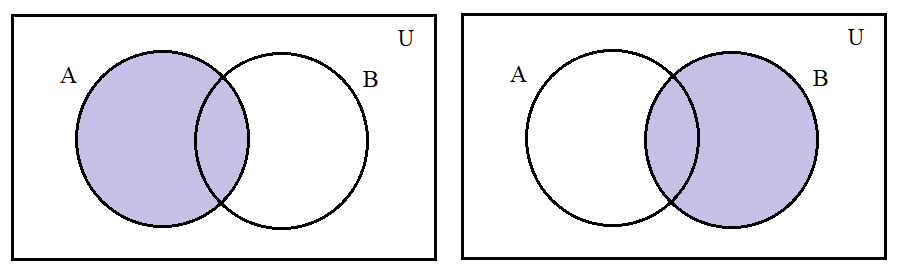
                                                                                                                             \[n(B)\]
                                                                                    \[n(A \cap B)\]

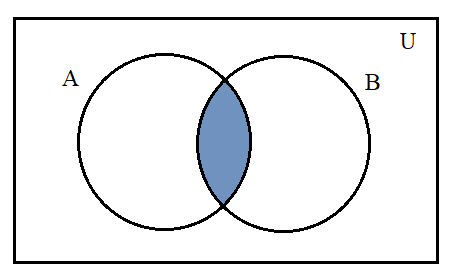
If we see that there was an overlap at the intersection part when we add \[n(A)\]& \[n(B)\]so, we will get two parts of \[n(A \cap B)\]. When we subtract one part of the term \[n(A \cap B)\]we will get\[n(A \cup B)\].
In this, we have the value of \[n(A),n(B)\& n(A \cup B)\] using this we can find the value of \[n(A \cap B)\].
Let us substitute the values we have in the formula \[n(A \cup B) = n(A) + n(B) - n(A \cap B)\].
\[n(A \cup B) = n(A) + n(B) - n(A \cap B)\]\[ \Rightarrow 410 = 285 + 195 - n(A \cap B)\]
Let us simplify this to find the value of\[n(A \cap B)\]. Let us take\[n(A \cap B)\] to the other side and shift \[410\] to the right side.
\[ \Rightarrow n(A \cap B) = 285 + 195 - 410\]
On simplifying this we get
\[ \Rightarrow n(A \cap B) = 480 - 410\]
\[ \Rightarrow n(A \cap B) = 70\]
Thus, we got the value of\[n(A \cap B) = 70\].
Now we can find the value of\[n(A' \cup B')\]. Let us now use the formula \[n(A' \cup B') = n(A \cap B)' = n(U) - n(A \cap B)\]and substitute the values of\[n(U)\]&\[n(A \cap B)\].
Let us first draw a Venn diagram.
We know that\[n(A' \cup B') = n(A \cap B)'\]. Let’s draw the Venn diagram for this.
                                                                        \[n(A' \cup B') = n(A \cap B)'\]

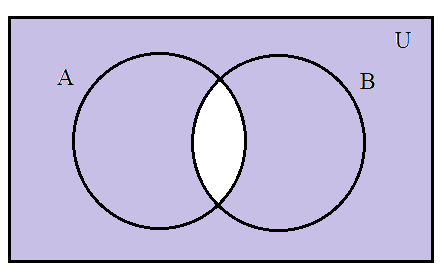
                                          \[n(U)\]

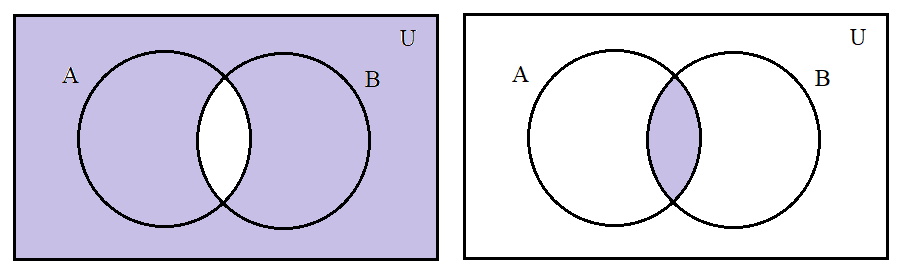
                                                                                                                                             \[n(A \cap B)\]
Thus, when we subtract \[n(A \cap B)\] from \[n(U)\] we get \[n(A' \cup B')\]or\[n(A \cap B)'\].
On substituting the values of\[n(U) = 500\& n(A \cap B) = 70\] in\[n(A' \cup B') = n(A \cap B)' = n(U) - n(A \cap B)\] we get
\[n(A' \cup B') = n(A \cap B)' = n(U) - n(A \cap B)\]\[ \Rightarrow 500 - 70\]
On simplifying this we get
\[ \Rightarrow n(A' \cap B') = 430\]
Thus, we have found the value of the term\[n(A \cap B) = 430\].

Note: It is important to choose the correct formula because there may be some formula giving the value that we need but they won’t contain the terms we have so we need to find the values that we don’t have and use that to find the value that we want.