Question

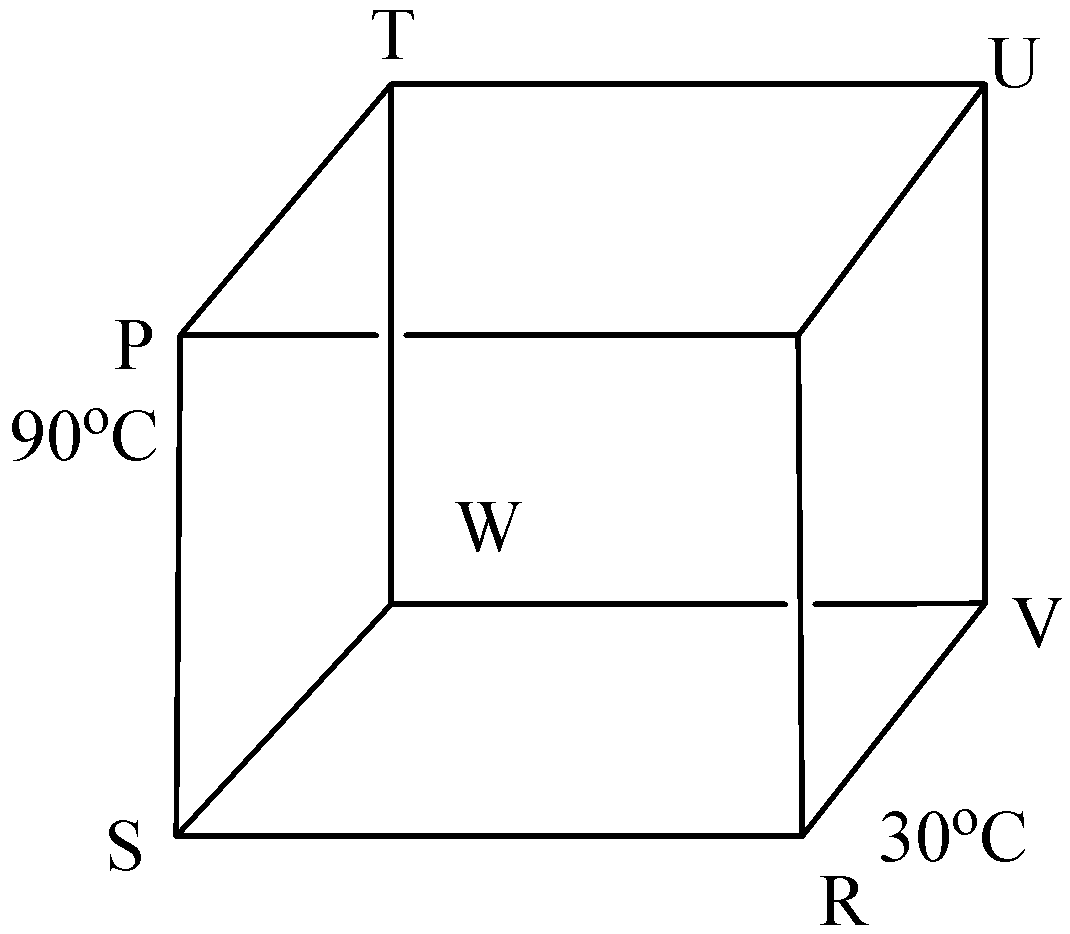
Given,\[12\] Identical rods made of the same material are arranged in the form of a cube. The temperature of 'P' and 'R' are maintained at \[90^\circ C\] and \[30^\circ C\] respectively. Then the temperature of point V, when steady state is reached is:

A.\[65^\circ C\]
B.\[60^\circ C\]
C.\[20^\circ C\]
D.\[50^\circ C\]

Answer 1

Hint: According to thermodynamics, in a steady state condition, the physical process or the system remains constant after the transformation or change. Which means, it is an unchanging condition. For example, if we take a chemical mix with different properties, and that chemical mix keeps that same properties, even after adding a change agent. And this is the example for steady state.

Complete answer:
The temperature of V is not equal to \[65^\circ C\]. Hence, option (A) is incorrect.
At steady state, the temperature does not become \[60^\circ C\]. Hence, the option (B) is incorrect.
The temperature of point V is not equal to \[20^\circ C\]. Hence, option (C) is incorrect.
Given, the temperature of P and R rods are \[90^\circ C\] and \[30^\circ C\] respectively. And here all the rods are identical. Therefore, the thermal conductivity of all the rods are equal. And it passes the same amount of heat through all the rods.
Let us consider the resistance of each rod is \[1\Omega \]
By calculation, we got the value of net resistance between P and R is \[\dfrac{3}{4}\Omega \]
 We need to find out the current which passed through P and coming out from R. Therefore,
\[I = \dfrac{V}{R}\]
According to current electricity, V is equal to the difference between the temperature of P and R rods. And R is the resistance between P and R, that is \[\dfrac{3}{4}\Omega \]. Substitute the values in above equation,
$I = \dfrac{{90 - 30}}{{\dfrac{3}{4}}}$
$ = \dfrac{{60}}{{\dfrac{3}{4}}}$
$ \Rightarrow I = \dfrac{{60 \times 4}}{3}$
On simplification we get,
$I = 80\Omega $
So, \[80\Omega \] of current will enter into P and exit from R. We know P and R maintain some potential and that is, \[90V\] and \[30V\] respectively. And the same current will pass through P and R.
Next we can find out the temperature of V in terms of voltage. Where resistance of V is equal to one and current passes through V is equal to \[10\Omega \], voltage is equal to \[60V\].
Hence,
\[I = (60 - 10) \times 1\]
On simplification we get,
$ \Rightarrow I = 50V$
Here, the electric current is replaced by heat and the temperature of point V, when steady state is reached, is equal to \[50^\circ C\].

Hence, the option (D) is correct.

Note:
We need to know that in the case of steady state, the state variables are always equal to the same or constant. And there will not be any change in their physical state, if we add any changing agent. And the steady state can be kept up by balancing the rate of substrate. But in the case of an unstable state, the variable should be changed in each interval of time.