Question

Given $x=2\cot t$ and $y=2{{\sin }^{2}}t$ for $0 < t < \dfrac{\pi }{2}$ , how do you find the Cartesian equation for this curve and state the domain?

Answer 1

Hint: To find the Cartesian equation for this curve, we have to find ${{\cot }^{2}}t$ from $x=2\cot t$ and ${{\csc }^{2}}t$ from $y=2{{\sin }^{2}}t$ so that we can substitute these in the formula ${{\csc }^{2}}t-{{\cot }^{2}}t=1$ . Then we will simplify the equation for y. To find a domain, we know that domain of a function is the set of all possible inputs for the function.

Complete step-by-step solution:
We are given that $x=2\cot t$ and $y=2{{\sin }^{2}}t$ for $0 < t < \dfrac{\pi }{2}$ . Let us consider $x=2\cot t$ . From this, we can find $\cot t$ as follows.
$\begin{align}
  & x=2\cot t \\
 & \Rightarrow \cot t=\dfrac{x}{2}...\left( i \right) \\
\end{align}$
Now, let us find ${{\cot }^{2}}t$ by squaring equation (i). We will get
$\begin{align}
  & \Rightarrow {{\left( \cot t \right)}^{2}}={{\left( \dfrac{x}{2} \right)}^{2}} \\
 & \Rightarrow {{\cot }^{2}}t=\dfrac{{{x}^{2}}}{4}...\left( ii \right) \\
\end{align}$
Now, let us consider $y=2{{\sin }^{2}}t$ . We know that $\csc x=\dfrac{1}{\sin x}$ . Hence, we can find ${{\csc }^{2}}t$ as follows.
$\begin{align}
  & y=2{{\sin }^{2}}t \\
 & \Rightarrow {{\sin }^{2}}t=\dfrac{y}{2} \\
 & \Rightarrow {{\csc }^{2}}t=\dfrac{1}{{{\sin }^{2}}t}=\dfrac{2}{y}...\left( iii \right) \\
\end{align}$
We know that ${{\csc }^{2}}t-{{\cot }^{2}}t=1$ . Hence from (ii) and (iii), we can write
$\dfrac{2}{y}-\dfrac{{{x}^{2}}}{4}=1$
We have to form an equation in y by solving the above equation. Let us take the second term of LHS to the RHS.
$\Rightarrow \dfrac{2}{y}=1+\dfrac{{{x}^{2}}}{4}$
 Now, we have to take the reciprocal of the above equation.
$\begin{align}
  & \Rightarrow \dfrac{1}{\dfrac{2}{y}}=\dfrac{1}{1+\dfrac{{{x}^{2}}}{4}} \\
 & \Rightarrow \dfrac{y}{2}=\dfrac{1}{1+\dfrac{{{x}^{2}}}{4}} \\
\end{align}$
Let us solve the denominator at the RHS of the above equation.
$\begin{align}
  & \Rightarrow \dfrac{y}{2}=\dfrac{1}{\dfrac{4+{{x}^{2}}}{4}} \\
 & \Rightarrow \dfrac{y}{2}=\dfrac{4}{4+{{x}^{2}}} \\
\end{align}$
We have to take 2 from LHS to RHS.
$\begin{align}
  & \Rightarrow y=2\times \dfrac{4}{4+{{x}^{2}}} \\
 & \Rightarrow y=\dfrac{8}{4+{{x}^{2}}}...\left( iv \right) \\
\end{align}$
Hence, the required Cartesian equation is $y=\dfrac{8}{4+{{x}^{2}}}$ .
Now, let us find the domain. We know that the domain of a function is the set of all possible inputs for the function. Hence, for the above equation, all real values are possible. Hence, the domain of the function is $x\in R$ .
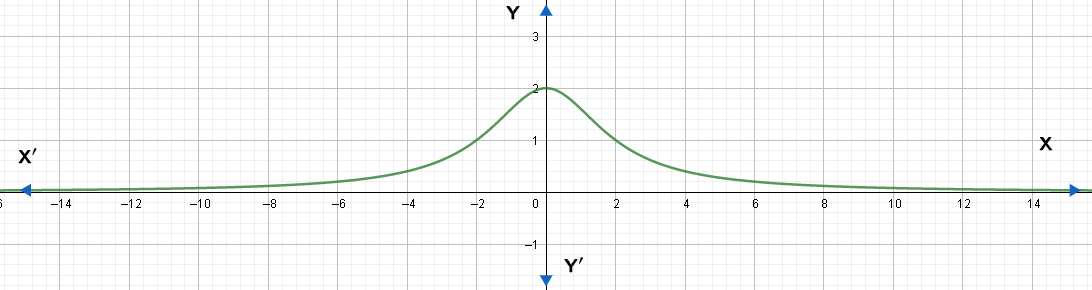
We can draw a graph of equation (iv) for different values of x.

Note: Students must know trigonometric identities to solve these problems. We can also draw a graph of $y=\dfrac{8}{4+{{x}^{2}}}$ by substituting different real values for x and finding the corresponding y values. The graph obtained is shown below.