Question

Given two isosceles triangles, ABC and DBC on the same base BC and vertices A and D, are on the same side of BC. If AD is extended to intersect BC at p, show that, AP is the perpendicular bisector of BC.

Answer 1

Hint: Use the congruence property of triangles, which is, two triangles are congruent if sides and angles of a triangle are equal to the corresponding sides and angle of the other triangle.

Complete step-by-step answer:
According to the question, the figure will be-

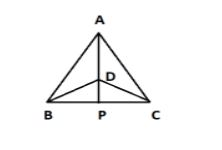
Given ABC and DBC are two isosceles triangles with base BC.
So, we will see the $\vartriangle ABC$ and $\vartriangle DBC$, since both the triangles are isosceles, therefore the two sides of an isosceles triangle are equal.
Therefore, in $\vartriangle ABC$, $AB = AC - (1) $ [sides of an isosceles triangle are equal]
In $\vartriangle DBC, DB = DC - (2) $[sides of an isosceles triangle are equal]
Now, see in triangles $\vartriangle ABC$ and $\vartriangle ACD$, we find the following congruence, which is stated below-
In $\vartriangle ABC$ and $\vartriangle ACD$

AB = AC [From (1)]
DB = DC [From (2)]
AD = AD [Common side]
$ \vartriangle ABC \cong \vartriangle ACD $

By SSS Test congruence, the two triangles, $\vartriangle ABC$ and $\vartriangle ACD$are congruent.
Using the congruence property, the two angles are also equal, i.e.,
$\therefore \angle BAD = \angle CAD - (1)$[Corresponding angle of congruent triangle]
Now we will see in $\vartriangle ABP$ and $\vartriangle ACP$,
$AB = AC$ [From (1), as these are the sides of an isosceles triangle]
$AP = AP$ [common side]
$\angle BAP = \angle CAP$ [From (3)]
$\vartriangle ABP \cong \vartriangle ACP$ [By SAS test of congruence]
Therefore, by SAS test of congruence we can also say that,
$BP = CP - (4)$ [corresponding pairs of congruent triangles]
$\angle APB = \angle APC - (5)$ [corresponding pairs of congruent triangles]
Now we will see whether $\vartriangle BDP$ and $\vartriangle CDP$are congruent.
Therefore, in $\vartriangle BDP$ and $\vartriangle CDP$, we have-
$DP = DC$ [From (1)]
$BP = CP$ [From (2)]
$DP = DP$ [common side]
$\therefore \vartriangle BDP \cong \vartriangle CDP$ are congruent triangles by SSS congruence.
Using the above result, i.e. $\vartriangle BDP \cong \vartriangle CDP$ , we can also say that,
$\therefore \angle BDP = \angle CDP$ [corresponding pairs of congruent triangles]
Since $\angle BDP = \angle CDP$ by SSS congruence, we can say that $AP$ bisects $\angle D$
Since, $\angle BAD = \angle CAD$ [From (3)], we can say that $AP$ bisects $\angle A$
This means AP is the angle bisector of both the angles, $\angle D$and $\angle A$.
Now use the property that the sum of angles formed on a straight line is equal to 180 degrees.
So, we can see that angle APB and angle APC are on the straight line, therefore their sum is equal to 180 degrees.
Hence, we can write -
$\angle APB + \angle APC = {180^ \circ }$ [Angle in a straight line is 180]
Since, $\angle APB = \angle APC$ by SAS congruence.
So, putting $\angle APB = \angle APC$ in the above equation, we get
$\angle APB + \angle APB = {180^ \circ }$ [From (5)]
Solving it further, we get-
$
  2\angle APB = {180^ \circ } \\
  \angle APB = {90^ \circ } \\
  \angle APB = \angle APC = {90^ \circ } \\
$
Now, we got the result that $\angle APB = \angle APC = {90^ \circ }$ , which concludes that AP is the perpendicular bisector of BC.

Note: Whenever this type of question appears, the way of solving should be by drawing the figure by using the information given in the question and then by using the concept of congruent triangle, step by step proceed towards the proof, since it is a lengthy solution, so be careful while writing the equations.