Question

Given two 4 digit numbers abcd and dcba. If a + d = b + c = 7, then their sum is not divisible by
(a) 7
(b) 11
(c) 101
(d) 111

Answer 1

Hint: To solve the question given above we will make use of the fact that when there are two four-digit number and the sum of their thousand’s place digit is less than 10, the sum of their hundred’s place digit is less than 10, the sum of their tens place digit is less than 10 and the sum of their unit place digit is less than 10, then the sum of the two four-digit number will be obtained as shown
\[\begin{align}
  & \text{ }\left[ {{x}_{1}} \right]\left[ {{x}_{2}} \right]\left[ {{x}_{3}} \right]\left[ {{x}_{4}} \right] \\
 & \underline{+\text{ }\left[ {{x}_{5}} \right]\left[ {{x}_{6}} \right]\left[ {{x}_{7}} \right]\left[ {{x}_{8}} \right]\text{ }} \\
 & \left[ {{x}_{1}}+{{x}_{5}} \right]\left[ {{x}_{2}}+{{x}_{6}} \right]\left[ {{x}_{3}}+{{x}_{7}} \right]\left[ {{x}_{4}}+{{x}_{8}} \right] \\
\end{align}\]
where \[\left( {{x}_{1}}+{{x}_{5}} \right),\left( {{x}_{2}}+{{x}_{6}} \right),\left( {{x}_{3}}+{{x}_{7}} \right),\left( {{x}_{4}}+{{x}_{8}} \right)\] all are less than 10. With the help of this, we will find the sum of abcd and dcba. After that, we will divide the sum by the numbers given in the option. If, after division, we get a remainder then that number will not be divisible by the sum.

Complete step-by-step answer:
To start with, we will make use of the fact that if there are two four-digit numbers of the form \[{{x}_{1}}{{x}_{2}}{{x}_{3}}{{x}_{4}}\] and \[{{x}_{5}}{{x}_{6}}{{x}_{7}}{{x}_{8}}\] such that \[\left( {{x}_{1}}+{{x}_{5}} \right),\left( {{x}_{2}}+{{x}_{6}} \right),\left( {{x}_{3}}+{{x}_{7}} \right),\left( {{x}_{4}}+{{x}_{8}} \right)\] all are less than 10, then the sum of these two numbers will be given by
\[\begin{align}
  & \text{ }\left[ {{x}_{1}} \right]\left[ {{x}_{2}} \right]\left[ {{x}_{3}} \right]\left[ {{x}_{4}} \right] \\
 & \underline{+\text{ }\left[ {{x}_{5}} \right]\left[ {{x}_{6}} \right]\left[ {{x}_{7}} \right]\left[ {{x}_{8}} \right]\text{ }} \\
 & \left[ {{x}_{1}}+{{x}_{5}} \right]\left[ {{x}_{2}}+{{x}_{6}} \right]\left[ {{x}_{3}}+{{x}_{7}} \right]\left[ {{x}_{4}}+{{x}_{8}} \right] \\
\end{align}\]
In our case, the numbers are abcd and dcba. The value of (a + d) is 7. The value of (b + c) is 7, the value of (c + b) is 7 and the value of (d + a) is 7. Thus, all these values are less than 10. So, the sum of abcd and dcba will be
\[\begin{align}
  & \text{ }a\text{ }b\text{ }c\text{ }d \\
 & \underline{+\text{ }d\text{ }c\text{ }b\text{ }a\text{ }} \\
 & \left[ a+d \right]\left[ b+c \right]\left[ c+b \right]\left[ d+a \right] \\
\end{align}\]
Now, it is given that a + d = b + c = 7. So, we will get,
\[\begin{align}
  & \text{ }a\text{ }b\text{ }c\text{ }d \\
 & \underline{+\text{ }d\text{ }c\text{ }b\text{ }a\text{ }} \\
 & \text{ }7777 \\
\end{align}\]
Thus, the sum of abcd and dcba is 7777. Now, we have to find out that 7777 is not divisible by which number. Now, we will check each option.
Option (a): 7
\[7777=7\times 1111+0\]
Here, the remainder is zero. So, 7777 is divisible by 7.
Option (b): 11
\[7777=11\times 707+0\]
Here, the remainder is zero. So, 7777 is divisible by 11.
Option (c): 101
\[7777=101\times 77+0\]
Here, the remainder is zero. So, 7777 is divisible by 101.
Option (d): 111
\[7777=111\times 70+7\]
Here, the remainder is not zero. So, 7777 is not divisible by 111.
Hence, option (d) is the right answer.

Note: The divisibility of 7777 can also be tested by doing prime factorization of 7777 which is shown below.

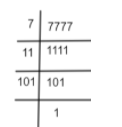
Thus, we can say that, \[7777=7\times 11\times 101.\] Thus, 7777 is only divisible by 7, 11, 101, 77, 707, 1111. Thus, 7777 is not divisible by 111.