Question

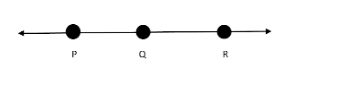
Given three collinear points $ P,Q $ and $ R $ . List all the line segments determined by these points.

A. $ \overline {PQ} $
B. $ \overline {PR} $
C. $ \overline {RQ} $
D. All of the above

Answer 1

Hint: In order to deal with this question we will use the concept that a line is the set of points between and beyond two points. A line is infinite in length. All points on a line are collinear points so we will obtain all the possible line segments from given points $ P,Q $ and $ R $ .

Complete step-by-step answer:
Given points are $ P,Q $ and $ R $

As we know that Three points \[A,{\text{ }}B\] and $ C $ are said to be collinear if they lie on the same straight line.
There points \[A,{\text{ }}B\] and $ C $ will be collinear if \[AB{\text{ }} + {\text{ }}BC{\text{ }} = {\text{ }}AC\], \[BA{\text{ }} + {\text{ }}AC{\text{ }} = {\text{ }}BC\]as is clear from the adjoining figure.
In general, three points \[A,{\text{ }}B\] and $ C $ are collinear if the sum of the lengths of any two line segments among $ AB,BC $ and $ CA $ is equal to the length of the remaining line segment.
And Line is the set of points between and beyond two points. A line is infinite in length. All points on a line are collinear points.
Here from the figure we have observed that
From point $ P $ and $ Q $ , a line segment is formed as $ \overline {PQ} $
Similarly, from point $ Q $ and $ R $ , a line segment is formed as $ \overline {RQ} $
And , from point $ P $ and $ R $ , a line segment is formed as $ \overline {PR} $
Therefore, The line segments determined by three collinear points $ P $ , $ Q $ and $ R $ are $ \overline {PQ} $ $ \overline {RQ} $ $ \overline {PR} $ because at least two points from a line segment which are collinear.

Hence the correct answer is option D.

Note: In general, three points \[A,{\text{ }}B\] and $ C $ are collinear if the sum of the lengths of any two line segments among $ AB,BC $ and $ CA $ is equal to the length of the remaining line segment, that is, either \[AB{\text{ }} + {\text{ }}BC{\text{ }} = {\text{ }}AC\] or \[AC{\text{ }} + CB{\text{ }} = {\text{ }}AB\] or \[BA{\text{ }} + {\text{ }}AC{\text{ }} = {\text{ }}BC\]. Throughout geometry, a set of points' collinearity is the property of their being lying on a single side. A set of points is said to be collinear, with this property. More generally , the term was used for objects in alignment, that is, items being "in a line" or "in a row".