Question

Given $\theta =\dfrac{19\pi }{6}$, how do you find $\sin \theta $?

Answer 1

Hint: We will use $\sin \left( \dfrac{\pi }{6} \right)=\dfrac{1}{2}$ to get to the right answer. Also, to simplify the angle we will convert \[\dfrac{19\pi }{6}=6\left( \dfrac{\pi }{2} \right)+\dfrac{\pi }{6}\] and solve it further. Moreover, to know about the presence of an angle is in which quadrant we have to take the help of a graph in which each angle will be $90{}^\circ $ apart.

Complete step-by-step answer:
We will consider the following diagram to solve this question.

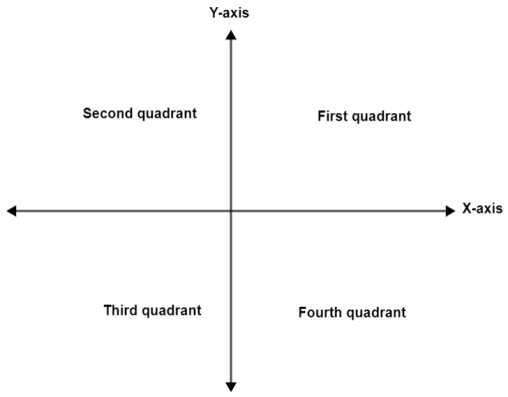
In this question, we can see the four quadrants. Now, we will find out that where the given angle lies in it. For this we need to simplify the angle $\theta =\dfrac{19\pi }{6}$. This can be done as follows,
\[\begin{align}
  & \theta =\dfrac{19\pi }{6} \\
 & \Rightarrow \theta =\dfrac{18\pi +\pi }{6} \\
 & \Rightarrow \theta =\dfrac{6\left( 3\pi \right)+\pi }{6} \\
 & \Rightarrow \theta =\dfrac{6\left( 3\pi \right)}{6}+\dfrac{\pi }{6} \\
 & \Rightarrow \theta =6\left( \dfrac{\pi }{2} \right)+\dfrac{\pi }{6}\,...(i) \\
\end{align}\]
Now, in order to find $\sin \left( \theta \right)$, we need to substitute equation (i) in it. Therefore, we get$\sin \left( \theta \right)=\sin \left( 6\left( \dfrac{\pi }{2} \right)+\dfrac{\pi }{6} \right)$. At this point we will move $\dfrac{\pi }{2}$ six times in the above figure. Thus, we get the following new diagram,

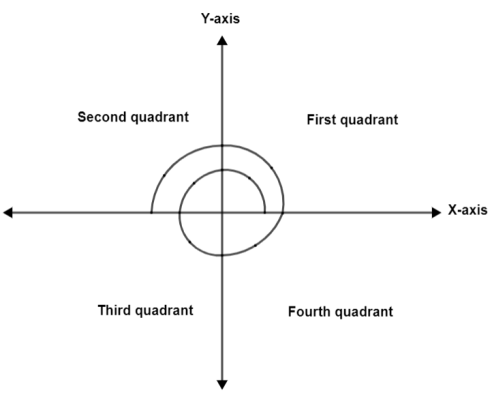
After this we are going to trace $\dfrac{\pi }{6}$ and stop when reached to the third quadrant. Thus, we get

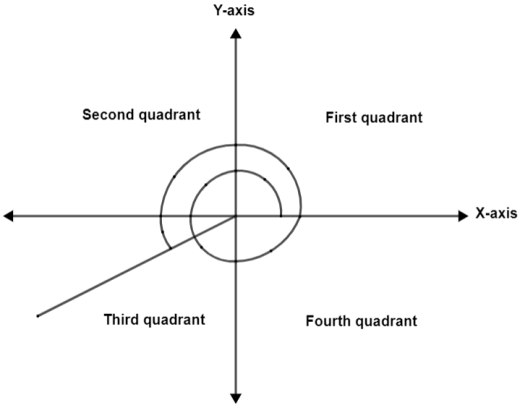
Since, in the third quadrant sine is always negative therefore, we will now have $\sin \left( \theta \right)=-\sin \left( \dfrac{\pi }{6} \right)$. As the value of $\sin \left( \dfrac{\pi }{6} \right)=\dfrac{1}{2}$ thus, we get $\sin \left( \theta \right)=-\dfrac{1}{2}$.
Hence, the value of $\sin \left( \theta \right)=-\dfrac{1}{2}$.

Note:We could have solve the problem with the following process,
\[\begin{align}
  & \theta =\dfrac{19\pi }{6} \\
 & \Rightarrow \theta =\dfrac{18\pi +\pi }{6} \\
 & \Rightarrow \theta =\dfrac{6\left( 3\pi \right)+\pi }{6} \\
 & \Rightarrow \theta =\dfrac{6\left( 3\pi \right)}{6}+\dfrac{\pi }{6} \\
 & \Rightarrow \theta =3\pi +\dfrac{\pi }{6} \\
\end{align}\]
From this method we would have traced $\pi $ instead of $\dfrac{\pi }{2}$ and get to the same answer. But in this case the formula would have used here be \[\sin \left( 3\pi +\dfrac{\pi }{6} \right)=-\sin \left( \dfrac{\pi }{6} \right)\]. Leading towards the right answer must be tricky here as in trigonometry, one small mistake can give wrong angle. This may result into getting no marks at all. The angle of $\pi $ taken here is $180{}^\circ $. This is how we have traced the above diagrams.