Question

Given the vertical height of the projectile at time t is \[y\text{ }=\text{ }4t\text{ }\text{- }5{{t}^{2}}\]and the horizontal distance covered is given by \[x\text{ }=\text{ }3t\]. Then what is the angle of projection with the horizontal?
 a) \[{{\tan }^{-1}}\dfrac{3}{5}\]
b) \[{{\tan }^{-1}}\dfrac{4}{5}\]
c) \[{{\tan }^{-1}}\dfrac{4}{3}\]
 d) \[{{\tan }^{-1}}\dfrac{3}{4}\]

Answer 1

Hint: In order to solve this question, we first need to calculate velocity along the \[x\] axis and \[y\] axis. After that we will find the velocity of the projectile and then calculate the angle of projection.

Complete step-by-step solution:
 let us draw the above problem to find the solution easily,

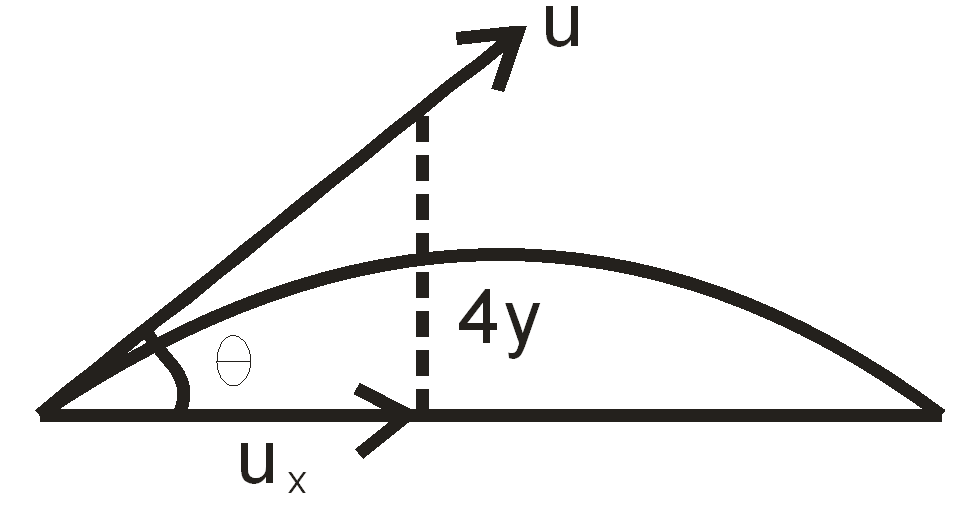
 According to the question , we get
 \[y\text{ }=\text{ }4t\text{ }\text{-}5{{t}^{2}}\] and
\[x\text{ }=\text{ }3t\]
Now, we have to calculate the velocity along \[x\]- axis,
\[{{v}_{x}}\Rightarrow \dfrac{dx}{dt}\Rightarrow 3m/s\]
Again , velocity along \[y\]- axis,
\[{{v}_{y}}\Rightarrow \dfrac{dy}{dt}\]
\[{{v}_{y}}\Rightarrow 4-10t\]
\[{{v}_{y}}_{t=0\sec}\Rightarrow 4m/s\]
Therefore, velocity of the projectile,
\[v\Rightarrow V_x\overrightarrow{i}+ V_y\overrightarrow{j}\]
\[v\Rightarrow \left( 3\overrightarrow{i}+4\overrightarrow{j} \right)m/s\]
\[\therefore \] Angle of projection,
\[\begin{align}
  & \tan \theta \Rightarrow \dfrac{V_y}{V_x} \\
 & \tan \theta \Rightarrow \dfrac{4}{3} \\
 & \theta \Rightarrow {{\tan }^{-1}}\left( \dfrac{4}{3} \right) \\
\end{align}\]
Therefore , option c is correct.

Note: Path of a projectile is known as trajectory, where range is known while the horizontal distance travels by the projectile. When the angle of projection is \[{{45}^{\circ }}\], the horizontal range becomes maximum .