Question

Given the central angle of the wedge on a pie graph, how do I find the percentage?

Answer 1

Hint: For conversion of the central angle into percentage, we first divide the central angle by ${{360}^{\circ }}$ and then multiply it with $100$ to make it a percentage.

Complete step-by-step answer:
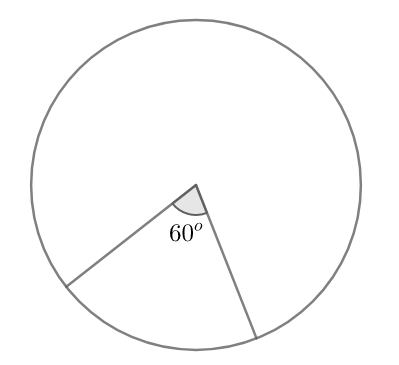
Portions can be expressed in several ways. It can be expressed “out of $100$ “known as percentage, or as ratios or other ways. Pie chart is a way of visualising portions. It is a pictorial representation of how much part of a thing is taken by another, for example how much portion of the hours of a day is taken by sleeping. Pie chart is nothing but a circle but various sectors marked on it. By sectors, we mean the portion of the circle bounded by two radii and the arc of the circle in between the radii. Now, since we have considered an arc of the circle, the arc will subtend an angle at the centre of the circle. This will be some angle less than or equal to ${{360}^{\circ }}$ . It will be equal to ${{360}^{\circ }}$ when the arc length will be equal to the perimeter of the circle and less than ${{360}^{\circ }}$ when the arc length will be less that the perimeter of the circle.
The share of the area of the circle covered by the sector will be the ratio of the angle subtended by it at the centre (or the central angle) to the total internal angle of the circle, i.e., ${{360}^{\circ }}$ . Let us take the central angle as ${{60}^{\circ }}$ . The ratio will then be,
$\dfrac{{{60}^{\circ }}}{{{360}^{\circ }}}=\dfrac{1}{6}$
This will be converted to a percentage by multiplying it with $100$ . This then becomes,
$\Rightarrow \dfrac{1}{6}\times 100\%=16.667\%$
Therefore, we have seen how we can convert a pie chart into a percentage.

Note: We should be careful while evaluating the ratio of angles. Students often take the denominator of the ratio to be ${{180}^{\circ }}$ instead of ${{360}^{\circ }}$ , which causes wrong answers. There is also a formula which is,
\[Percentage\text{ }=\text{ }\dfrac{\left( Central\text{ }angle \right)}{{{360}^{\circ }}}\times 100\%\]