
Given that, for all the real values of x, the expression
a. 0 and 2
b. -1 and 1
c. -1 and 0
d.
Answer
504.6k+ views
Hint: We will first assume
Complete step-by-step solution:
It is given in the question that for all the real values of x, the expression
Let us first assume the expression
On transposing all the terms on the LHS to the RHS, we get,
Now, it is a quadratic equation and we know that in a quadratic equation, the discriminant
So, from the quadratic equation, we have a = (1 - y), b = -2 (1 + y) and c = 4 (1 – y).
So, we have the discriminant,
On taking 4 common from both the terms, we get,
We know that
On opening the bracket, we get,
On further simplifying, we get,
On multiplying both the sides by (-1), we get,
Here, the sign of the inequality changes as we have multiplied the expression with a negative number. Now, we can split -10y as -9y –y, so we get,
Now, we will plot
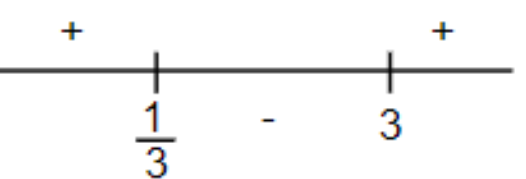
If we put 0 in
Again, if we put 1 in
And we put 4 in
Hence, we can show the number line as,
Thus, we get a region
Also,
This means that the range does not depend on x, but it depend on y.
Now, we have been given the expression,
Let us assume that
Now, if we compare
Thus, the range of the expression,
Hence, option (d) is the correct answer.
Note: Most of the students make mistake after multiplying the expression,
Complete step-by-step solution:
It is given in the question that for all the real values of x, the expression
Let us first assume the expression
On transposing all the terms on the LHS to the RHS, we get,
Now, it is a quadratic equation and we know that in a quadratic equation, the discriminant
So, from the quadratic equation, we have a = (1 - y), b = -2 (1 + y) and c = 4 (1 – y).
So, we have the discriminant,
On taking 4 common from both the terms, we get,
We know that
On opening the bracket, we get,
On further simplifying, we get,
On multiplying both the sides by (-1), we get,
Here, the sign of the inequality changes as we have multiplied the expression with a negative number. Now, we can split -10y as -9y –y, so we get,
Now, we will plot
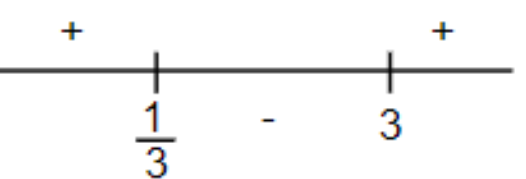
If we put 0 in
Again, if we put 1 in
And we put 4 in
Hence, we can show the number line as,
Thus, we get a region
Also,
This means that the range does not depend on x, but it depend on y.
Now, we have been given the expression,
Let us assume that
Now, if we compare
Thus, the range of the expression,
Hence, option (d) is the correct answer.
Note: Most of the students make mistake after multiplying the expression,
Recently Updated Pages
Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Trending doubts
Explain why it is said like that Mock drill is use class 11 social science CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE




