Question

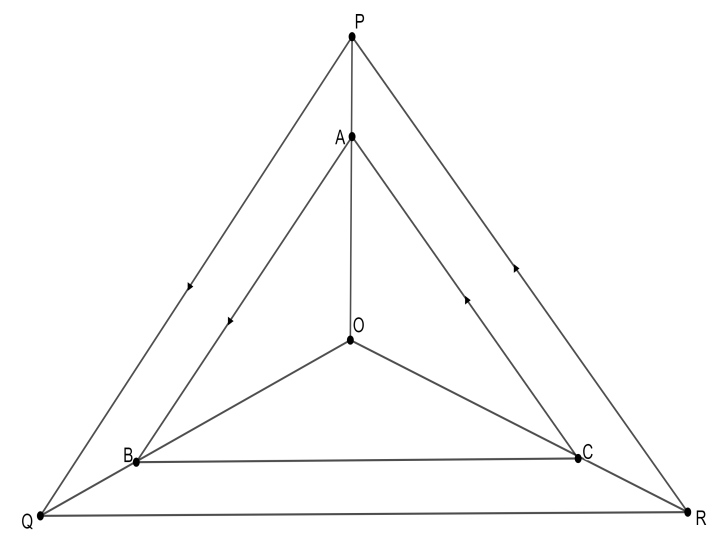
Given that $AB\parallel PQ$ and $AC\parallel PR$, show that $BC\parallel QR$.

Answer 1

Hint: We will show that $\Delta OAB\sim \Delta OPQ$ by using the fact that $AB\parallel PQ$. Then we will show that $\Delta OAC\sim \Delta OPR$ since $AC\parallel PR$. After that we will show that $\Delta OBC\sim \Delta OQR$. Next, we will use the fact that if two corresponding angles are congruent, then the two lines cut by the transversal must be parallel.

Complete step by step answer:
We will first consider the two triangles $\Delta OAB$ and $\Delta OPQ$. We know that $AB\parallel PQ$. Looking at segment OP as a transversal, we get that $\angle OAB=\angle OPQ$ because they are corresponding angles. Similarly, considering segment OQ as the transversal, we have $\angle OBA=\angle OQP$. As $\angle AOB=\angle POQ$, since it is a common angle. Hence, by AAA test, we have $\Delta OAB\sim \Delta OPQ$. Therefore, we have the following ratio of sides,
\[\dfrac{OB}{OQ}=\dfrac{OA}{OP}\] .
Now, we will consider the two triangles $\Delta OAC$ and $\Delta OPR$. We know that $AC\parallel PR$. Considering segment OR as a transversal, we have $\angle OCA=\angle ORP$, since they are the corresponding angles. Similarly, we consider segment OP as a transversal. So that we have $\angle OAC=\angle OPR$. Again, we have a common angle, therefore, we also have $\angle AOC=\angle POR$ . Therefore, by AAA test, we can conclude that $\Delta OAC\sim \Delta OPR$. Hence, we have the ratio of the sides of these triangles as follows,
\[\dfrac{OA}{OP}=\dfrac{OC}{OR}\] .
Now we consider $\Delta OBC$ and $\Delta OQR$. We have a common angle, so $\angle BOC=\angle QOR$. Since \[\dfrac{OB}{OQ}=\dfrac{OA}{OP}\] and \[\dfrac{OA}{OP}=\dfrac{OC}{OR}\], we have \[\dfrac{OB}{OQ}=\dfrac{OC}{OR}\]. Hence, by SAS test, we have $\Delta OBC\sim \Delta OQR$. So, we have $\angle OBC=\angle OQR$. We know that if two corresponding angles are congruent, then the two lines cut by the transversal must be parallel. Hence, the transversal is segment OQ and $BC\parallel QR$.
Hence, proved.

Note: The angles and ratios of sides should be written carefully. Many minor mistakes are possible, especially while showing that two triangles are similar. The converse statements of the properties of transversal and two parallel lines are very useful in such questions. Properties of similar triangles are the key aspect of this question.