Question

Given right triangle ABC, with AB = 4 , BC = 3 and CA = 5. Circle, $\omega $ passes through $A$ and is tangent to $BC$ at $C$. What is the radius of $\omega $?

Answer 1

Hint: Here, a right angle triangle $ABC$ is given with $AB = 4$, $BC = 3$ and $CA = 5$. Also, a circle $\omega $ passes through $A$ and a tangent is drawn at $C$, perpendicular to $BC$.
 The tangent to a circle is nothing but a line that touches the circle at a single point.
We are asked to calculate the radius of the circle.
First, we need to draw a graph representing the given information.
Formula to be used:
The formula to calculate the distance between two points to determine the radius is as follows.
\[r = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
Where $r$ is the radius of a circle.
The equation of a circle is as follows.
${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$
Where $r$ is the radius of a circle and $(h,k)$ is the center of a circle.
Also, ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$

Complete step-by-step solution:
 We shall represent the given information in a diagram as shown.

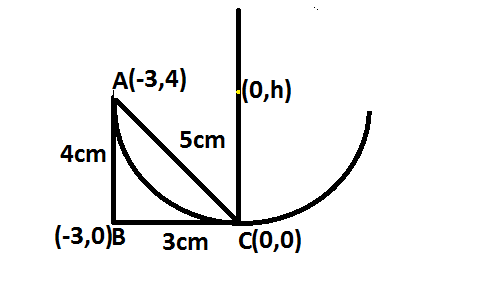
Here, we need to find the coordinates of A and B using the given information.
The distance between the points $\left( {0,0} \right)$ and $\left( {0,h} \right)$ is the radius of the circle.
Now, using the formula \[r = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \], we get,
\[r = \sqrt {{{\left( {0 - 0} \right)}^2} + {{\left( {h - 0} \right)}^2}} \]
\[r = \sqrt {{h^2}} \]
Hence, $r = h$ is the radius of the circle.
Here, $(h,k) = \left( {0,h} \right)$ is the center of the circle.
Now, we need to apply the formula.
The equation of a circle is as follows.
${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$
Where $r$ is the radius of a circle and $(h,k)$ is the center of a circle.
Hence, we get,
${\left( {x - 0} \right)^2} + {\left( {y - h} \right)^2} = {h^2}$ ……$\left( 1 \right)$
Here, the equation of a circle passes through a point $A\left( { - 3,4} \right)$.
Hence, the equation $\left( 1 \right)$ becomes,
${\left( { - 3 - 0} \right)^2} + {\left( {4 - h} \right)^2} = {h^2}$
$ \Rightarrow 9 + {\left( {4 - h} \right)^2} = {h^2}$
Using the formula ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$, we get
$9 + {4^2} - 2 \times 4 \times h + {h^2} = {h^2}$
$ \Rightarrow 9 + 16 - 8h + {h^2} = {h^2}$
 $ \Rightarrow 25 - 8h + {h^2} = {h^2}$
$ \Rightarrow 25 - 8h + {h^2} - {h^2} = 0$
$ \Rightarrow 25 - 8h = 0$
$ \Rightarrow 25 = 8h$
$ \Rightarrow h = \dfrac{{25}}{8}$
Therefore, the radius of the circle $\omega $ is $\dfrac{{25}}{8}$.

Note: The tangent to a circle is nothing but a line that touches the circle at a single point and we know that radius is always perpendicular to the tangent at the touching point. We must be clear enough to represent the given information in a diagram so that we can solve the problem easily.
Hence, the radius of the circle $\omega $ is $\dfrac{{25}}{8}$ .