Question

Given: $\overline{AB}$ and $\overline{CD}$ intersect at $O$ and the endpoints of $\overline{AB}$ and $\overline{CD}$ are on circle $O$.
Prove: $\overline{AC}\cong \overline{BD}$

Answer 1

Hint: We can apply the cosine rule to find the angles $\angle AOC$ and $\angle BOD$ and hence establish a relation between the sides $AC$ and $BD$.

Complete Step-by-Step Solution:
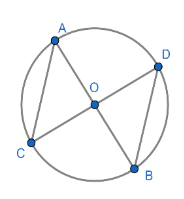
It is given in the question that $\overline{AB}$and $\overline{CD}$ intersect at $O$. It is also given that the endpoints of $\overline{AB}$ and $\overline{CD}$ are on circle $O$.
So, we can draw a figure from the data given in the question as shown below.

Let us consider that the circle has a radius $r$ and has its centre at point $O$. Since $O$ is the centre of the circle and the points $A,B,C,D$ lie on the circumference of the circle, we can obtain the following relation:
$OA=OB=OC=OD=r$
Let us assume that the angle $\angle AOC=\theta $.
Since $\angle AOC$ and $\angle BOD$ are vertically opposite angles, they will be the same. Therefore, we can write that
$\angle AOC=\theta $
$\angle BOD=\theta $
Now, let us consider a triangle with sides $a,b,c$ and angle $\alpha $as shown in the figure below,

$\cos \alpha =\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}................\left( i \right)$
The above formula is called the cosine rule. Generally, we know that the cosine of any angle in a right-angled triangle is equal to the ratio of the base to the hypotenuse. But the cosine rule can be applied to any triangle, be it an acute triangle, obtuse triangle or a right-angled triangle.
Using the cosine rule $\left( i \right)$ in $\angle AOC$, we get
$\cos \theta =\dfrac{{{r}^{2}}+{{r}^{2}}-{{\left( AC \right)}^{2}}}{2{{r}^{2}}}$
$\Rightarrow 2{{r}^{2}}\cos \theta =2{{r}^{2}}-{{\left( AC \right)}^{2}}$
$\Rightarrow {{\left( AC \right)}^{2}}=2{{r}^{2}}-2{{r}^{2}}\cos \theta ............\left( ii \right)$
Using the cosine rule $\left( i \right)$ in $\angle BOD$, we get
$\cos \theta =\dfrac{{{r}^{2}}+{{r}^{2}}-{{\left( BD \right)}^{2}}}{2{{r}^{2}}}$
$\Rightarrow 2{{r}^{2}}\cos \theta =2{{r}^{2}}-{{\left( BD \right)}^{2}}$
 $\Rightarrow {{\left( BD \right)}^{2}}=2{{r}^{2}}-2{{r}^{2}}\cos \theta ................(iii)$
If we compare the equations $\left( ii \right)$ and $\left( iii \right)$, we get that
${{\left( AC \right)}^{2}}={{\left( BD \right)}^{2}}$
$\Rightarrow \left( AC \right)=\left( BD \right)$
Therefore, it states that the length of$AC~$is equal to the length of $BD$.
$\overline{AC}\cong \overline{BD}$
Hence proved.

Note: This question uses the concepts of circles and also requires the knowledge of cosine rule, which is a concept of the properties of a triangle. In order to find the relation between $AC$ and $BD$, one has to use the cosine rule.