Question

Given inside a circle, whose radius is equal to 13 cm, is a point M at a distance 5 cm from the centre of the circle. A chord AB=25 cm is drawn through M. The lengths of the segments into which the chord AB is divided by the point M is:
(a) 12, 13
(b) 14, 11
(c) 15, 10
(d) 16, 9

Answer 1

Hint: Start by drawing the diagram of the situation given in the figure along with a line joining the centre of the circle and bisecting the chord AB. Also, join the points A and B with the centre of the circle using two line segments. Use the property that the line from the centre bisects the chord is perpendicular to the chord as well and use the Pythagoras theorem to get the length of the line bisecting the chord. Also, you know the distance of point M from the centre. So, again use the Pythagoras theorem to get the distance between M and the centre point of the chord. Add the result you get to one half of the chord and subtract from the other half to get the answer.

Complete step-by-step answer:
Let us start the solution to the above question by drawing the diagram of the situation given in the question along with required diagrams.

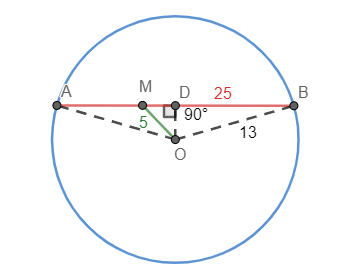
According to the question AB=25cm, OA=OB=13cm=radius, OM=5cm. Also, we know that the line from the centre bisects the chord is perpendicular to the chord as well. So, we can say that $\angle ODA=90{}^\circ $ .
So, we can say that ODA and ODM are right angled triangles. Also, $DB=AD=\dfrac{25}{2}cm$ .
Now we will apply Pythagoras theorem in $\Delta ODA$ .
${{\left( perpendicular \right)}^{2}}+{{\left( base \right)}^{2}}={{\left( hypotenuse \right)}^{2}}$
$\Rightarrow O{{D}^{2}}+A{{D}^{2}}=O{{A}^{2}}$
$\Rightarrow O{{D}^{2}}+{{\left( \dfrac{25}{2} \right)}^{2}}={{13}^{2}}$
$\Rightarrow O{{D}^{2}}=169-\dfrac{625}{4}......(i)$
Again we will apply Pythagoras theorem in $\Delta ODM$ .
${{\left( perpendicular \right)}^{2}}+{{\left( base \right)}^{2}}={{\left( hypotenuse \right)}^{2}}$
$\Rightarrow O{{D}^{2}}+D{{M}^{2}}=O{{M}^{2}}$
Substituting the value of the square of OD from equation (i). On doing so, we get
$169-\dfrac{625}{4}+D{{M}^{2}}={{5}^{2}}$
$\Rightarrow D{{M}^{2}}=25-169+\dfrac{625}{4}=-144+\dfrac{625}{4}$
$\Rightarrow D{{M}^{2}}=\dfrac{-576+625}{4}=\dfrac{49}{4}$
$\Rightarrow DM=\sqrt{\dfrac{49}{4}}=\dfrac{7}{2}=3.5cm$
So, AM=AD-DM=12.5-3.5=9cm and BM=BD+DM=16cm.
So, the answer is option (d).

Note: In the question, the key is the diagram and the constructions. Also, the use of property related to the perpendicular bisector of the chord of a circle passing through its centre is also the only method. If you have seen in the question that we have not found the exact value of OD instead found the square of it, because we were not needing OD but the need was its square to use in the Pythagoras theorem so, we worked wisely and saved some time.