Question

Given here are some figures:
Classify each of them on the basis of the following
(i) Simple curve
(ii) Simple closed curve
(iii) Polygon
(iv) Convex polygon
(v) Concave polygon
(vi) Not a curve

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

Answer 1

Hint: To solve this question, we need to first understand what various categories given to us are and what are the conditions a curve needs to satisfy to fall into specific categories. Thus, we will define each of the given five categories and segregate the figures into those categories.

Complete step by step answer:
We are given 8 figures and there are six categories in which we need to segregate the curves.
The first category given to us is a simple curve.
A curve is said to be a simple curve if it does not intersect itself. There can be edges to the curve and it can be a loop with no start or end, but two arms or sides of the curve should not intersect each other. Such a curve is a simple curve.
The following figures are simple curves, as they do not intersect themselves.
(1), (2), (5), (6) and (7)

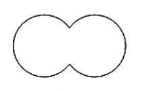
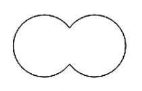
Next category is a simple closed curve. All the simple curves which do not have a well defined starting and ending point and form a closed loop are simple closed curves. All the simple curves with us are simple closed curves. That is curve (1), (2), (5), (6) and (7)

A polygon is defined as a closed figure with well defined sides and vertices. Polygon is exclusively made of straight lines and does not contain any curved arms or sides. From the figures given to us, only (1) and (2) can qualify as polygons.

A polygon is said to be a convex polygon if all the internal angles of the polygon are less than or equal to 90°. Out of the two polygons we have classified, the figure (2) is a convex polygon.

A polygon is said to be a concave polygon if at least one of its internal angles is obtuse angle or more than 90°. Figure (1) is a concave polygon.

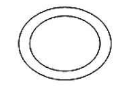
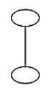
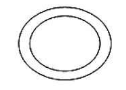
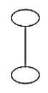
So far, figures (3), (4) and (8) are not categorized. This is because they are not curves. In figure (3), there is an ellipse inside an ellipse and they cannot be categorized as a single curve. In figure (4), the arms of the star intersect each other and thus it is also not a curve. The figure (8) contains two loops and one straight line and it is not a single curve of any kind. Thus, these three will be categorized as not curved.

Note: Students can categorise the figures just by looking at them. The other definition of convex polygon is that all the diagonals are internal and lie in the area inside the polygon. The case is totally opposite with concave polygons, which can have external diagonals.