Question

Given \[\cos A=0.6\]; Find all other trigonometric ratios for angle A.

Answer 1

Hint: In this problem, we are given the value of one of the trigonometric ratios, with which we have to find the remaining. We can first write 0.6 in fraction, from which we can get the adjacent side and the hypotenuse side as \[\cos A=\dfrac{adjacent}{hypotenuse}\]. We can then use the Pythagoras theorem to find the adjacent side and we can find the other ratios answer.

Complete step by step answer:
Here we are given the value of one of the trigonometric ratios, with which we have to find the remaining.
We are given \[\cos A=0.6\].
We can now write it as,
\[\Rightarrow \cos A=\dfrac{6}{10}=\dfrac{3}{5}\]
We know that secant is the inverse of cosine, we can write it as,
\[\Rightarrow \sec A=\dfrac{5}{3}\]
We know that \[\cos A=\dfrac{adjacent}{hypotenuse}\].
Here we have two sides, and we can find the other using the Pythagoras theorem.
\[\Rightarrow opposite=\sqrt{{{5}^{2}}-{{3}^{2}}}=\sqrt{16}=4\]

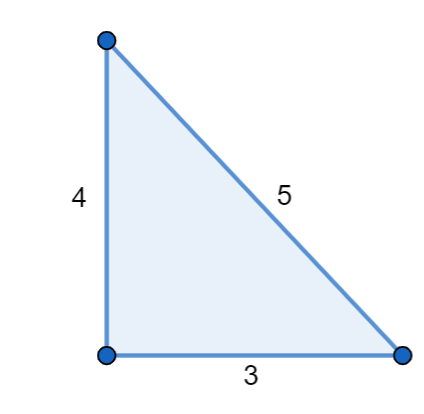
Now we have Adjacent side = 3, Opposite side = 4 and Hypotenuse = 5.
We know that,
\[\Rightarrow \sin A=\dfrac{opposite}{hypotenuse}=\dfrac{4}{5}\]
We know that cosecant is the inverse of sine, so we can write it as
\[\Rightarrow \cos ecA=\dfrac{5}{4}\]
We know that,
\[\Rightarrow \tan A=\dfrac{opposite}{adjacent}=\dfrac{4}{3}\]
We know that cotangent is the inverse of tangent, so we can write it as
\[\Rightarrow \cot A=\dfrac{3}{4}\]
Therefore, the required trigonometric ratios are,
\[\begin{align}
  & \sin A=\dfrac{4}{5} \\
 & \cos ecA=\dfrac{5}{4} \\
 & \tan A=\dfrac{4}{3} \\
 & \cot A=\dfrac{3}{4} \\
 & \sec A=\dfrac{5}{3} \\
\end{align}\]

Note: We should always remember the trigonometric ratio formulas for every angles such as sine is opposite side by hypotenuse, cosine is adjacent side by hypotenuse and tangent is opposite side by adjacent side, where secant is the inverse of cosine, cotangent is inverse of tangent and secant is the inverse of sine.