Question

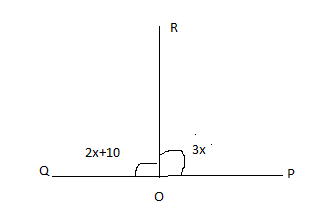
Given, \[\angle POR = 3x\,\,and\,\,\angle QOR = 2x + 10\] , find the value of x for which POQ will be a line. (figure)

Answer 1

Hint: As we can see we are given the angles \[\angle POR\,\,and\,\,\angle QOR\] , and we need to find the value of x so that POQ will be a line; which means POQ will form a straight angle i.e. \[{180^0}\] . A linear pair of angles is formed when two lines intersect lines. The measure of straight angle is \[{180^0}\] . So a linear pair of angles add up to \[{180^0}\] .

Complete step-by-step answer:
Given data: \[\angle POR = 3x\,\,and\,\,\angle QOR = 2x + 10\] , we need to find out the value of x, so that POQ will be a straight line.
To calculate x for which POQ will be a straight line.
Let us consider, P,O,Q are in one line. If POQ forms a line, then the angles \[\angle POR\,\,and\,\,\angle QOR\] will be the two adjacent angles.
We know, a linear pair is defined as a pair of adjacent angles that adds up to \[{180^0}\] .
i.e.:$\angle POR\, + \angle QOR = {180^0}\\
 \Rightarrow 3x + 2x + 10 = {180^0}\\
 \Rightarrow 5x + 10 = {180^0}$
Now, subtract the constant part by taking it to the right side.
$\Rightarrow 5x = {(180 - 10)^0}\\
 \Rightarrow 5x = {170^0}\\
 \Rightarrow x = {34^0}$
.: The required value of x is equal to \[{34^0}\] , for which POQ will be in a straight line.

Note: Students just need to keep one thing in mind is the formula of the linear pair of the angles. Students do not be confused between adjacent angles and supplementary angles. Supplementary angles are two angles whose measures add up to \[{180^0}\] (degree) whereas adjacent angles are two angles that happen to lie next to each other so that they can combine a larger angle.