Question

Given an equilateral triangle, how would you find its area using: The Pythagorean Theorem?

Answer 1

Hint: Imagine or construct an equilateral triangle. Mark its known values. The angles of an equilateral triangle are always equal to $ 60 $ degrees. We know the regular formula to find the area of any triangle, it is: $ \dfrac{1}{2} \times b \times h $ ; where $ b = $ base of triangle and $ h = $ height of that triangle. We need to relate it to the Pythagorean theorem, that theorem says that hypotenuse of a triangle can be represented by this formula: $ {l^2} = \sqrt {{a^2} + {b^2}} $ , here $ l = $ length of hypotenuse of the triangle (side of triangle opposite the right angle), $ a,b = $ length of remaining two sides

Complete step-by-step answer:
Our goal is to give a formula using Pythagorean Theorem to find out the area of an equilateral triangle. We must see how we can relate the original formula of area of a triangle to the Pythagorean Theorem.
Now let us first note down what we know from the given data:
We know that the triangle is equilateral, so it’s sides are all the same. Let the side of the triangle be $ s $ , then all the sides will be length $ s $ .
Then we know that in an equilateral triangle, all the inner angles are $ {60^ \circ } $ so there is no hypotenuse as of now, so let us construct a median from any one corner to the center of the opposite edge. In this manner we have constructed an angle of $ {90^ \circ } $ in the triangle so we can assume that one of the sides is the hypotenuse.
In the above mentioned way we can make a triangle that looks like this:

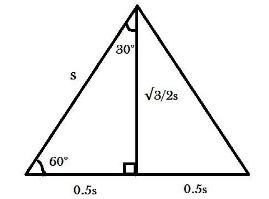
Now we can write the Pythagorean theorem for the constructed triangle.
 $ \Rightarrow {(\dfrac{1}{2} \times s)^2} + {h^2} = {s^2} $
Let us separate the value of $ {h^2} $ , to find the value of height of triangle;
\[ \Rightarrow {h^2} = {s^2} - {(\dfrac{1}{2} \times s)^2}\]
\[ \Rightarrow {h^2} = {s^2} - (\dfrac{1}{4}) \times {s^2}\]
\[ \Rightarrow {h^2} = \dfrac{3}{4} \times {s^2}\]
\[\therefore h = \dfrac{{\sqrt 3 }}{2} \times s\]
But the area of the complete triangle can be written in this way:
 $ \Rightarrow A = 2 \times \dfrac{1}{2} \times \dfrac{1}{2}s \times \dfrac{{\sqrt 3 }}{2}s $
 $ \Rightarrow A = \dfrac{{\sqrt 3 }}{4} \times {s^2} $
So the equilateral triangle’s area using the Pythagorean Theorem is: $ \dfrac{{\sqrt 3 }}{4} \times {s^2} $ .
So, the correct answer is “ $ \dfrac{{\sqrt 3 }}{4} \times {s^2} $ .”.

Note: There are many other ways in which we can find the area of a triangle, one other way is using Heron's formula. In order for us to use this formula, we should know the sides of the triangle before calculating its area. If we know this we can use the Heron’s formula that says;
 $ Area = \sqrt {s \times (s - a) \times (s - b) \times (s - c)} $ ; here the value of
  $ a,b,c = $ length of each side , $ s $ = $ \dfrac{1}{2} \times (a + b + c) $
Using this formula, if the area is already given we can find the sides of the triangle also.