Question

Given, ABCD is a trapezium in which \[AB\parallel DC\] and \[AD = BC\]. If P, Q, R, S be the mid-points of BA, BD, CD and CA respectively. Show that PQRS is a Rhombus?

Answer 1

Hint: A trapezium is a quadrilateral with four sides and one pair of parallel sides. As we can see in Trapezium \[AB\parallel DC\] and \[AD = BC\] and P, Q, R, S are the mid points in which all the sides of a rhombus are congruent. Hence in this way we can prove that PQRS is Rhombus.

Complete step by step answer:
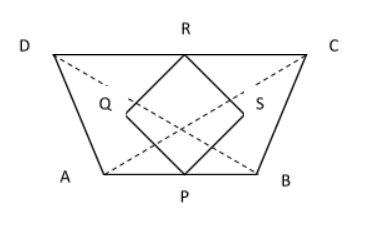
ABCD is a trapezium in which \[AB\parallel DC\] and \[AD = BC\] and P, Q, R, S are the mid-points of BA, BD, CD and CA as shown in the figure.
Hence, we need to show that PQRS is a Rhombus.
Considering \[\Delta ABC\], \[\Delta ADC\], \[\Delta BCD\] and \[\Delta ABD\] from the Trapezium with PQRS as mid points.
In \[\Delta ABC\], P, S are the mid points of AB, AC respectively.
So, \[PS||BC\] and
\[PS = \dfrac{1}{2}BC\]………………………1
Similarly, in \[\Delta ADC\],
\[RS = \dfrac{1}{2}AD = \dfrac{1}{2}BC\]……………….2
In \[\Delta BCD\],
\[RQ = \dfrac{1}{2}BC\] ……………………… 3
Similarly, in \[\Delta ABD\],
\[QP = \dfrac{1}{2}AD = \dfrac{1}{2}BC\] …………………. 4
Therefore from 1, 2, 3, and 4 we get
\[PQ = QR = RS = SP\]
Since all sides are equal, PQRS is a rhombus.

Note:
As in a Trapezium \[AB\parallel DC\] and \[AD = BC\] with PQRS as mid points we get to know that all four of its sides of Rhombus are congruent as rhombus is a type of parallelogram, and what distinguishes its shape is that all four of its sides are congruent.
Some key points to be noted are:
In Rhombus all four sides are congruent.
The diagonals bisect vertex angles of Rhombus, and hence these are known as perpendicular bisectors.
The consecutive angles in the rhombus are supplementary and the Diagonals are perpendicular to each other respectively.