Question

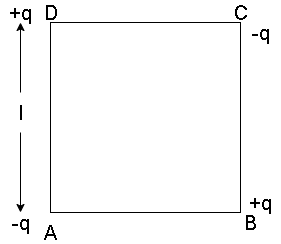
Given, ABCD is a square frame of side $l$ . The force at B if charges as shown in figure are placed at the corners of the square will be:

A.$\dfrac{{{q^2}(2\sqrt 2 - 1)}}{{4\pi {\varepsilon _o}2{l^2}}}$
B.$\dfrac{{{q^2}(2\sqrt 2 + 1)}}{{4\pi {\varepsilon _o}{l^2}}}$
C.$\dfrac{{{q^2}(2\sqrt 2 - 1)}}{{4\pi {\varepsilon _o}{l^2}}}$
D.$\dfrac{{{q^2}(2\sqrt 2 - 1)}}{{4\pi {\varepsilon _o}2{l^2}}}$

Answer 1

Hint: It should be noticed that the force of attraction or repulsion between two charges acts along the line between the two charges. Also like charges repel each other and unlike charges attract each other. The magnitude of force acting on the charges can be known by using Coulomb's Law.

Complete answer:
Step I:
According to Coulomb's law the force acting on any two charged particles depends directly on the magnitude of their charges and varies inversely as the square of distance between them.
Force acts on charge B due to the charges A,C and D. The forces between two charges separated by a distance is given by
$F = \dfrac{1}{{4\pi {\varepsilon _o}}}.\dfrac{{{q_1}{q_2}}}{{{r^2}}}$
Force acting on the charge B due to individual charge A will act along the line AB and is given by
${F_A} = \dfrac{1}{{4\pi {\varepsilon _o}}}.\dfrac{{q.( - q)\overrightarrow A }}{{{l^2}}}$
Or $\dfrac{1}{{4\pi {\varepsilon _o}}}.\dfrac{{{{( - q)}^2}}}{{{l^2}}}$
Step II:
Similarly force due to charge C will act along line BC and is given by,
${F_C} = \dfrac{1}{{4\pi {\varepsilon _o}}}.\dfrac{{q.( - q)}}{{{l^2}}}.\overrightarrow A $
Or $\dfrac{1}{{4\pi {\varepsilon _o}}}.\dfrac{{( - {q^2})}}{{{l^2}}}$
Force on charge D dueto charge at A will act along line DB and is given by
${F_D} = \dfrac{1}{{4\pi {\varepsilon _o}}}.\dfrac{{q.q}}{{{l^2}}}.\overrightarrow A $
Or $\dfrac{1}{{4\pi {\varepsilon _o}}}.\dfrac{{{q^2}}}{{2{l^2}}}$
Step III:
The force acting on the charge B due to A and C charge will act along line DB towards D.
In the square the diagonals will be AC and BD and both of them will have the same lengths.
Therefore,
$AC = BD = \sqrt {{{(AC)}^2} + {{(BD)}^2}} $
Or$ = \sqrt {{l^2} + {l^2}} $
Or $ = \sqrt 2 l$
Step IV:
Resultant force acting on Charge B due to the diagonals AC and BD is given by
${F_{AC}} = {F_{BD}}$
Therefore it can be written that,
${F_{AC}} = \dfrac{1}{{4\pi {\varepsilon _o}}}.[\dfrac{{{q^2}}}{{{{(\sqrt 2 l)}^2}}} + \dfrac{{{{( - q)}^2}}}{{{{(\sqrt 2 l)}^2}}}]$
\[ = \dfrac{1}{{4\pi {\varepsilon _o}}}.\dfrac{{2{{( - q)}^2}}}{{\sqrt 2 {l^2}}}\]
$ = \dfrac{1}{{4\pi {\varepsilon _o}}}.\dfrac{{\sqrt 2 {{( - q)}^2}}}{{{l^2}}}$
Step V:
Force acting on charge B due to AC and D is given by
${F_{net}} = {F_{AC}} - {F_D}$
Or \[\sqrt 2 \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{{{( - q)}^2}}}{{{l^2}}} + \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{{q^2}}}{{2{l^2}}}\]
= $\dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{{{(q)}^2}}}{{{l^2}}}(\sqrt 2 - \dfrac{1}{2})$
=$\dfrac{{{q^2}(2\sqrt 2 - 1)}}{{4\pi {\varepsilon _o}.2{l^2}}}$

Therefore option A is the right answer.

Note:
It is already told that the force varies inversely with the square of the distance between the charges. Therefore, if the distance between the charges is doubled, then the force of attraction or repulsion will get weaker. The force will decrease by one fourth of the original value.