Question

Given, $ABC$ is an equilateral triangle of side $2a$. Find each of its altitudes.

Answer 1

Hint: First we draw a equilateral triangle of side $2a$. Also, we draw altitudes perpendicular to the opposite sides. All interior angles of an equilateral triangle are equal in measure. Then, we use trigonometric properties to find the value of altitudes.

Complete step by step answer:
First we draw an equilateral triangle $ABC$ of side $2a$. Also, we draw perpendicular altitudes $AD,BE$ and $CF$ to the opposite sides. The altitudes drawn in an equilateral triangle are medians.
We have to find the length of all altitudes.

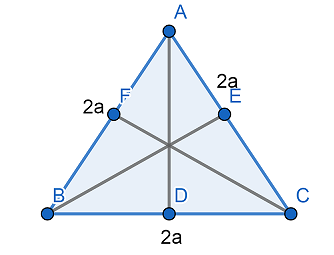
As we know that measure of all interior angles of an equilateral triangle is $60{}^\circ $.
To find the length of the altitudes we use trigonometric properties.
First we consider $\Delta ADC$, we know that the measure of $\angle ACD=60{}^\circ $ and $AD$ is perpendicular to $BC$. So, the $\angle ADC=90{}^\circ $
When we use the property of sine function in right angle triangle $ADC$, we get
$\sin \theta =\dfrac{\text{Perpendicular}}{\text{hypotenuse}}$
We have $\theta =60{}^\circ $
So, $\sin 60{}^\circ =\dfrac{AD}{AC}$
We know that $\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$
So, when we substitute the value, we get
$\begin{align}
  & \dfrac{\sqrt{3}}{2}=\dfrac{AD}{a} \\
 & \Rightarrow AD=\dfrac{\sqrt{3}}{2}a \\
\end{align}$
So, the length of each altitude is $\dfrac{\sqrt{3}}{2}a$.

Note:
Alternatively we can find altitudes using the congruence property of triangles. We prove the triangles are similar using congruence, which states that if two right triangles, hypotenuse and one side of one triangle are equal to hypotenuse and one side of another triangle, then the two triangles are congruent. Then, we apply Pythagora's theorem to find the altitudes.