
Given \[AB\] of length \[3.9cm,\] construct \[PQ\] such that the length of \[PQ\] is twice that of \[AB.\] Verify by measurement.
Answer
583.8k+ views
Hint: Construct a Line and mark the point PX such that length of PX is equal to AB. On the same line also make XQ which also have length equal to AB.
Complete step-by-step answer:
Since it is a construction problem students are asked to bring a ruler, pencil and compass for drawing the desired line segment.
If we try to understand the statement of the problem, we are required to construct a Line segment which is double the length of the given Line segment.
In such types of Questions we generally follow the same process where a certain length of line segment is given and some multiple of length of the given line segment is being asked to draw.
Let us jump straight to problem turning
It is given to us that AB is of the length \[3.9\,cm\]. Use the ruler and pencil to draw a Line segment of length \[3.9\,cm\] as follows.
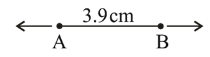
This length will be used in later parts of the problem. Now we need to draw a line PQ such that the length of PQ is twice that of AB.
\[\underline{PQ=2\times AB}\]
We are going to follow the steps mentioned below.
\[1)\] Use the ruler and pencil to draw the straight line l. On this straight line mark the point P as shown.

\[2)\] Use the Compass & Measure \[AB\] which is \[3.9\,cm\]
Figure
\[3)\] Now keep the same length in compass and with point P as center, draw an arc on the line l.
Figure
In this way we get the line \[\text{PX}\] which is \[3.9\,cm\].
\[\text{4)}\] Keep the same length in compass with point \[\text{X}\] as center, again cut an arc on the line l cutting \[\text{17}\] at point \[\text{Q}\].
Such that \[XQ=3.9\,\,cm\]
Therefore \[PQ=PX+XQ\]
\[=3.9+3.9=7.8\,\,cm\]
Therefore \[PQ\] is twice that of \[AB\].
\[PQ=2AB\]
Note: For drawing a line segment say PQ which is let say n times the given line segment say AB i.e. \[PQ=nAB,\] we have to draw a line segment starting with point P and make n number of cuts from compass of length equal to AB, starting from point P keeping the previous cut as the center of arc for the new cut.
Complete step-by-step answer:
Since it is a construction problem students are asked to bring a ruler, pencil and compass for drawing the desired line segment.
If we try to understand the statement of the problem, we are required to construct a Line segment which is double the length of the given Line segment.
In such types of Questions we generally follow the same process where a certain length of line segment is given and some multiple of length of the given line segment is being asked to draw.
Let us jump straight to problem turning
It is given to us that AB is of the length \[3.9\,cm\]. Use the ruler and pencil to draw a Line segment of length \[3.9\,cm\] as follows.
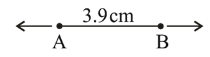
This length will be used in later parts of the problem. Now we need to draw a line PQ such that the length of PQ is twice that of AB.
\[\underline{PQ=2\times AB}\]
We are going to follow the steps mentioned below.
\[1)\] Use the ruler and pencil to draw the straight line l. On this straight line mark the point P as shown.

\[2)\] Use the Compass & Measure \[AB\] which is \[3.9\,cm\]
Figure
\[3)\] Now keep the same length in compass and with point P as center, draw an arc on the line l.
Figure
In this way we get the line \[\text{PX}\] which is \[3.9\,cm\].
\[\text{4)}\] Keep the same length in compass with point \[\text{X}\] as center, again cut an arc on the line l cutting \[\text{17}\] at point \[\text{Q}\].
Such that \[XQ=3.9\,\,cm\]
Therefore \[PQ=PX+XQ\]
\[=3.9+3.9=7.8\,\,cm\]
Therefore \[PQ\] is twice that of \[AB\].
\[PQ=2AB\]
Note: For drawing a line segment say PQ which is let say n times the given line segment say AB i.e. \[PQ=nAB,\] we have to draw a line segment starting with point P and make n number of cuts from compass of length equal to AB, starting from point P keeping the previous cut as the center of arc for the new cut.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




