Question

Given A, B, C and D are four masses each of mass M lying on the vertices of a square of side ‘a’. They always move along a common circle with velocity v. Find v so that they always remain on the vertices of the square –
A. \[\sqrt{\dfrac{GM(2\sqrt{2}+1)}{2\sqrt{2}a}}\]
B. \[\sqrt{\dfrac{GM(\sqrt{2}+1)}{2a}}\]
C. \[\sqrt{\dfrac{GM\sqrt{2}(2+1)}{a}}\]
D. None of the above

Answer 1

Hint: The formulae used to solve this problem are centrifugal force and Newton’s law of motion formulae. We will equate the net resultant force to the centrifugal force. Then, we will rearrange the terms of the equation to find the expression in terms of velocity v.

Formula used:
\[{{F}_{c}}=\dfrac{m{{v}^{2}}}{r}\]
\[F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\]

Complete step by step solution:
The formulae used are given as follows.
\[{{F}_{c}}=\dfrac{m{{v}^{2}}}{r}\]
The above equation represents the formula for computing the centrifugal force.
Where m is the mass of the object, v is the velocity of the object and r is the radius of the path.
\[F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\]
The above equation represents the formula for computing Newton’s law of gravitation.
Where \[{{m}_{1}},{{m}_{2}}\] are the masses of the objects, G is the gravitational constant and r is the distance between the objects.
From the data, we have the data as follows.
A, B, C and D are four masses each of mass M lying on the vertices of a square of side ‘a’.
They always move along a common circle with velocity v.
As, the side of a square given to be equal to ‘a’, thus, the length of the diagonal of the square becomes ‘\[\sqrt{2}a\]’.
The radius of the circle will be equal to the half the value of the diagonal of the square. So, the radius of the circle will be,
\[\begin{align}
  & r=\dfrac{\sqrt{2}a}{2} \\
 & \Rightarrow r=\dfrac{a}{\sqrt{2}} \\
\end{align}\]
Consider a figure representing the A, B, C and D are four masses each of mass M lying on the vertices of a square of side ‘a’.

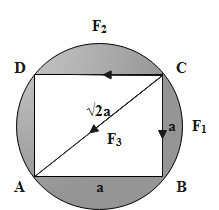
The above figure represents the forces \[{{F}_{1}},{{F}_{2}}\]acting along the sides of a square and \[{{F}_{3}}\] representing the resultant force of these two forces.
The magnitude of these forces will be equal to each other, that is,
\[|{{F}_{1}}|=|{{F}_{2}}|\]
Therefore, the net force equation can be written as follows.
\[F={{F}_{3}}+\sqrt{2}{{F}_{1}}\]
This force equals the centrifugal force that holds the A, B, C and D are four masses each of mass M back on the vertices of the square. So, we get,
\[{{F}_{3}}+\sqrt{2}{{F}_{1}}=\dfrac{m{{v}^{2}}}{r}\]
Now represent the forces in terms of Newton's law of gravitation.
\[\dfrac{G{{m}^{2}}}{{{(\sqrt{2}a)}^{2}}}+\sqrt{2}\dfrac{G{{m}^{2}}}{{{a}^{2}}}=\dfrac{m{{v}^{2}}}{a}\sqrt{2}\]
Cancel out the common terms.
\[\begin{align}
  & \dfrac{Gm}{a{{(\sqrt{2})}^{2}}}+\sqrt{2}\dfrac{Gm}{a}=\sqrt{2}{{v}^{2}} \\
 & \Rightarrow \dfrac{Gm}{2a}+\sqrt{2}\dfrac{Gm}{a}=\sqrt{2}{{v}^{2}} \\
\end{align}\]
Continue the further calculation and
\[\begin{align}
  & \dfrac{Gm}{a}\left( \dfrac{1}{2}+\sqrt{2} \right)=\sqrt{2}{{v}^{2}} \\
 & \Rightarrow \dfrac{Gm}{a}\left( \dfrac{1+2\sqrt{2}}{2} \right)=\sqrt{2}{{v}^{2}} \\
\end{align}\]
Represent the above equation in terms of the velocity. So, we get,
\[\begin{align}
  & {{v}^{2}}=\dfrac{Gm(1+2\sqrt{2})}{2\sqrt{2}a} \\
 & \Rightarrow v=\sqrt{\dfrac{Gm(1+2\sqrt{2})}{2\sqrt{2}a}} \\
\end{align}\]
\[\therefore \] The value of the v so that the masses A, B, C and D each of mass M always remain on the vertices of the square is \[v=\sqrt{\dfrac{Gm(1+2\sqrt{2})}{2\sqrt{2}a}}\].
As the value of the velocity is \[v=\sqrt{\dfrac{Gm(1+2\sqrt{2})}{2\sqrt{2}a}}\].

Thus, the option (A) is correct.

Note:
In order to make the masses remain on the vertices of the square, the centrifugal force must be acting on them continuously. So, we have equated the centrifugal force to the net forces acting on the masses. The radius of the circle along which the centrifugal force works equals half the value of the diagonal of the square.