Question

Give two different examples of pair of:
i. Similar figures
ii. Non-similar figures

Answer 1

Hint: Use the definition of similar figures to differentiate between similar and non-similar figures and give the examples accordingly.

Complete step-by-step answer:
We will first write the examples of similar figures, therefore consider,
Similar figures:
Before we write the examples of similar figures we should know its definition given below,
Definition:
Two figures are said to be similar if their corresponding angles are equal and the corresponding sides are in proportion i.e. the figures having the same shape are called Similar Figures.
We will write the examples of similar figures,
A pair of square:

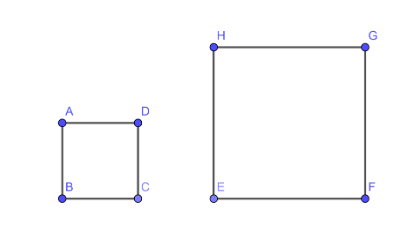
As we know that all the sides of a square are always equal and all the angles are of $90{}^{\circ }$. Therefore the corresponding angles of any two squares are always equal and their corresponding sides will always be in proportion. Therefore this is an example of a similar figure.
Similarly we can prove in case of equilateral triangles, and you can easily check it from figure also.

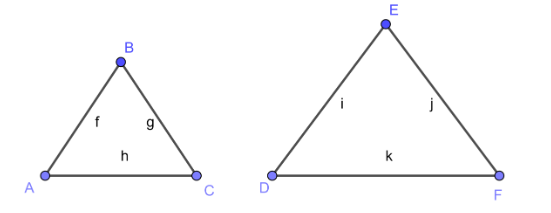
As we all know that the equilateral triangles have all sides equal and all the angles equal to $60{}^{\circ }$, therefore this is also an example of similar figures.
We will first write the examples of similar figures, therefore consider,
Non-similar figures:
Before we write the examples of non-similar figures we should know its definition given below,
Definition:
If there is no factor of similarity between the two figures of or the figures not obeying the conditions of similar figures are Non-similar Figures.
As it is very simple to identify non-similar figures therefore we will directly write the examples,
Pair of an Isosceles triangle and an equilateral triangle
As the corresponding angles of above two triangles are unequal therefore they are the examples of non-similar figures.
Pair of a triangle and a square.
As there is not even an equal number of sides in the above two figures therefore ultimately they are the example of non-similar figures.

Note: You should know that the congruent figures are also similar as their ratio of corresponding sides will be equal to 1 i.e. they are in proportion.