
Give the possible expression for the length and breadth of each of the following rectangles, in which their areas are given:
(i) Area: \[25{a^2} - 35a + 12\]
(ii) Area: \[35{y^2} + 13y - 12\]
Answer
572.7k+ views
Hint: Area of a rectangle is given as \[A = l \times b\], where \[l\] is the length of the rectangle and \[b\] is its breadth. The area is defined as the space occupied by a flat shape (two-dimensional) or the surface of an object. The area of a figure is denoted as the unit square that covers the surface of a closed figure.
In the question, two polynomial equations are given whose degree is 2, hence the number of roots of the equation will be two only, which will be the length and breadth of the rectangle. To determine the area of the rectangle, we need to determine the roots of the given equation and then multiply the roots to get the area of the rectangle.
Complete step-by-step answer:
(i) \[25{a^2} - 35a + 12\]
The area of the rectangle is given as \[25{a^2} - 35a + 12\] which is a quadratic equation and its two roots are the length and breadth of the rectangle.
Hence factorizing by splitting the middle term,
\[
A = 25{a^2} - 35a + 12 \\
= 25{a^2} - 15a - 20a + 12 \\
= 5a\left( {5a - 3} \right) - 4\left( {5a - 3} \right) \\
= \left( {5a - 4} \right)\left( {5a - 3} \right) \\
\]
Hence we can say the area\[A = l \times b = \left( {5a - 4} \right)\left( {5a - 3} \right)\]
Length\[ = \left( {5a - 3} \right)\] and Breadth\[ = \left( {5a - 4} \right)\]. At the same time vice-versa also holds true.
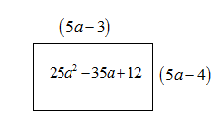
(ii) \[35{y^2} + 13y - 12\]
By using the method of factorization by splitting the middle term, we get:
\[
A = 35{y^2} + 13y - 12 \\
= 35{y^2} + 28y - 15y - 12 \\
= 7y\left( {5y + 4} \right) - 3\left( {5y + 4} \right) \\
= \left( {5y + 4} \right)\left( {7y - 3} \right) \\
\]
Hence we can say the area\[A = l \times b = \left( {5y + 4} \right)\left( {7y - 3} \right)\]
Length \[ = \left( {5y + 4} \right)\] and Breadth\[ = \left( {7y - 3} \right)\]. At the same time the vice-versa also holds true.
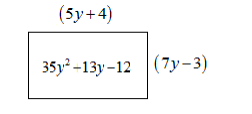
Note: A rectangle is a two-dimensional figure with four straight sides and four right angles, with unequal adjacent sides and equal parallel sides. In general, we can choose the length to be the greater sides of the two while the breadth as the smaller one.
In the question, two polynomial equations are given whose degree is 2, hence the number of roots of the equation will be two only, which will be the length and breadth of the rectangle. To determine the area of the rectangle, we need to determine the roots of the given equation and then multiply the roots to get the area of the rectangle.
Complete step-by-step answer:
(i) \[25{a^2} - 35a + 12\]
The area of the rectangle is given as \[25{a^2} - 35a + 12\] which is a quadratic equation and its two roots are the length and breadth of the rectangle.
Hence factorizing by splitting the middle term,
\[
A = 25{a^2} - 35a + 12 \\
= 25{a^2} - 15a - 20a + 12 \\
= 5a\left( {5a - 3} \right) - 4\left( {5a - 3} \right) \\
= \left( {5a - 4} \right)\left( {5a - 3} \right) \\
\]
Hence we can say the area\[A = l \times b = \left( {5a - 4} \right)\left( {5a - 3} \right)\]
Length\[ = \left( {5a - 3} \right)\] and Breadth\[ = \left( {5a - 4} \right)\]. At the same time vice-versa also holds true.
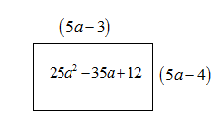
(ii) \[35{y^2} + 13y - 12\]
By using the method of factorization by splitting the middle term, we get:
\[
A = 35{y^2} + 13y - 12 \\
= 35{y^2} + 28y - 15y - 12 \\
= 7y\left( {5y + 4} \right) - 3\left( {5y + 4} \right) \\
= \left( {5y + 4} \right)\left( {7y - 3} \right) \\
\]
Hence we can say the area\[A = l \times b = \left( {5y + 4} \right)\left( {7y - 3} \right)\]
Length \[ = \left( {5y + 4} \right)\] and Breadth\[ = \left( {7y - 3} \right)\]. At the same time the vice-versa also holds true.
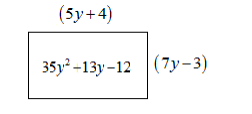
Note: A rectangle is a two-dimensional figure with four straight sides and four right angles, with unequal adjacent sides and equal parallel sides. In general, we can choose the length to be the greater sides of the two while the breadth as the smaller one.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the full form of pH?





