Question

Give the four lines with the equations
\[\begin{align}
  & x+2y-3=0 \\
 & 3x+4y-7=0 \\
 & 2x+3y-4=0 \\
 & 4x+5y-6=0 \\
\end{align}\]
A. they are all concurrent.
B. they are the sides of a quadrilateral.
C. only three lines are concurrent.
D. none of the above.

Answer 1

Hint: If all the given lines pass through the same point, then they are concurrent. To form the quadrilateral, no three lines can have a common point and more than two lines should not be parallel to each other, then the given lines are sides of the quadrilateral.

Complete step-by-step solution:
From the question, we were given four equations of lines
\[x+2y-3=0\]………………(1)
\[3x+4y-7=0\]………..…..(2)
\[2x+3y-4=0\]…………….(3)
\[4x+5y-6=0\]…………….(4)
By these equations we have to find out whether these lines form quadrilateral or concurrent or only three of these lines are concurrent.
First of all, let us check whether these lines are concurrent or not.
If all the given lines pass through a common point then they are concurrent.
Now consider equation (1) and (2) , from these equations try to get a common point.
From equation (1) we can write \[x=3-2y\]
Now substitute \[x=3-2y\] in equation (2)
\[\Rightarrow 3(3-2y)+4y-7=0\]
On simplification we get
\[\Rightarrow y=1\]
now put \[y=1\]in equation (1) to get \[x\]value.
\[\Rightarrow x+2y-3=0\]
\[\Rightarrow x+2(1)-3=0\]
\[\Rightarrow x=1\]
\[\left( 1,1 \right)\] in the intersection point of \[x+2y-3=0\] and \[3x+4y-7=0\].
Now put \[\left( 1,1 \right)\] in \[2x+3y-4\]
\[\Rightarrow 2x+3y-4\]
\[\Rightarrow 2+3-4\]
\[\Rightarrow 1\]
After substituting \[\left( 1,1 \right)\] in \[2x+3y-4\] we got \[1\] which is not equal to zero.
So \[2x+3y-4\] does not pass through\[\left( 1,1 \right)\].
So, these lines are not concurrent.
Now consider\[2x+3y-4=0\] and \[4x+5y-6=0\]
From \[4x+5y-6=0\] we can write \[x=\frac{6-5y}{4}\]
Now put \[x=\frac{6-5y}{4}\] in \[2x+3y-4=0\]
\[\Rightarrow 2x+3y-4=0\]
\[\Rightarrow 2\left( \frac{6-5y}{4} \right)+3y-4=0\]
After simplification we get
\[\Rightarrow y=2\]
Now put \[y=2\] in \[2x+3y-4=0\] to get \[x\] value
\[\Rightarrow 2x+3y-4=0\]
\[\begin{align}
  & \Rightarrow 2x+3(2)-4=0 \\
 & \Rightarrow 2x+6-4=0 \\
\end{align}\]
On simplification we get
\[\Rightarrow x=-1\]
\[(-1,2)\] is the intersection point of \[2x+3y-4=0\] and \[4x+5y-6=0\].
Now put \[(-1,2)\] in \[x+2y-3\] we get
\[\begin{align}
  & \Rightarrow -1+2\left( 2 \right)-3 \\
 & \Rightarrow -1+4-3 \\
 & \Rightarrow 0 \\
\end{align}\]
So \[x+2y-3=0\]passes through \[(-1,2)\].
Now put \[(-1,2)\] in \[3x+4y-7=0\]
\[\Rightarrow 3x+4y-7=0\]
\[\begin{align}
  & \Rightarrow 3\left( -1 \right)+4\left( 2 \right)-7 \\
 & \Rightarrow -3+8-7 \\
 & \Rightarrow -2 \\
\end{align}\]
We got \[-2\] which is not equal to zero, so \[3x+4y-7=0\]does not passes through\[(-1,2)\]
From this, we came to know that \[x+2y-3=0\], \[2x+3y-4=0\], \[4x+5y-6=0\] passes through
\[(-1,2)\] and \[3x+4y-7=0\] does not pass through \[(-1,2)\]. So only three lines are concurrent.

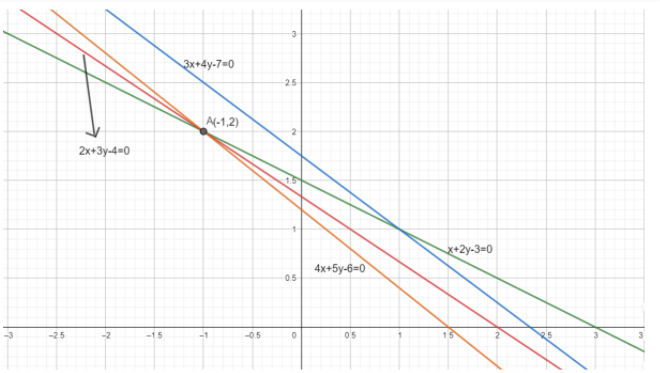
So, option C is the correct answer.

Note: Students should know the conditions for the lines to form a quadrilateral and some basic concepts regarding concurrency of lines. We should avoid calculation mistakes to get the correct answer.