Question

Give reasons for the following.
Squares, rectangles, parallelograms are all quadrilaterals.

Answer 1

Hint: We solve this question by explaining what each of these shapes are and how they are quadrilaterals. We give reasons by stating the properties of each one of the shapes and checking if it satisfies the condition for a figure required to be a quadrilateral.

Complete step-by-step solution:
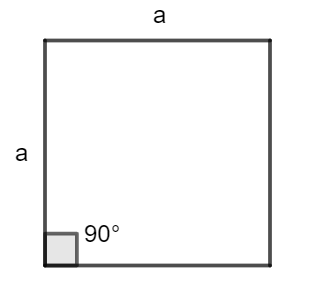
In order to solve this question, let us consider each of the shapes given one by one and state out their properties. The first shape given is a square. We know that a square is a closed figure such that all four sides of the square are equal. Also, we know that the 4 angles of the square are all equal and are equal to $90{}^\circ .$ This is given by the square in the figure of each side a.

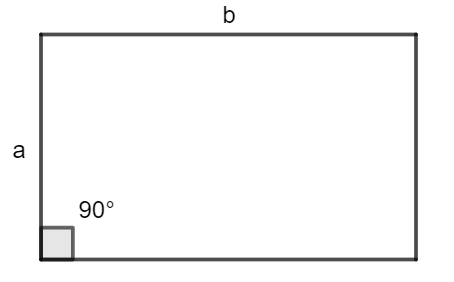
Next, we consider the rectangle. A rectangle is a closed figure such that the opposite sides are equal in length. The longest side is called the length and its opposite side is equal to it too. The shortest side is called the breadth and its opposite side is of the same length. This has a similar angle measurement compared to that of a square. Here, in a rectangle each of the 4 angles are $90{}^\circ .$ So, we can also say that the square is a special case of a rectangle where the length and breadth are the same. We have a rectangle as shown in the figure given by a length of b and breadth of a.

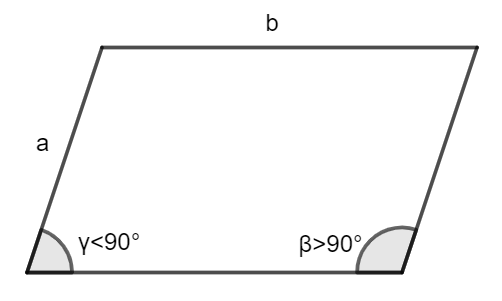
Next, we have the parallelogram. It is a closed figure having opposite sides parallel and equal to each other. It is similar to a rectangle except that its angles need not be $90{}^\circ .$ It has angles of any measure but its opposite angles are equal. We could say a special case of a parallelogram is a rectangle where all angles are equal to $90{}^\circ .$ This is shown in the figure below.

A quadrilateral is any closed figure having four sides. Since the above three figures all have four sides and are closed figures, hence we can say that squares, rectangles, parallelograms are all quadrilaterals.

Note: We need to know the basic figures in geometry and their properties. It is important to note that the sum of all angles inside the closed figure needs to add up to $360{}^\circ .$ This is one more property of all closed figures be it a four-sided or five-sided or n-sided figure.