Question

Give proof of the Pythagoras’ theorem?

Answer 1

Hint: Pythagoras’ theorem is inevitably one of the most important theorems in the field of geometry. We provide here one of the most famous proofs of the Pythagoras’ theorem, which is the first of Euclid’s two proofs. The proof is sometimes referred to as “Brides Chair”.
Outline of the proof:
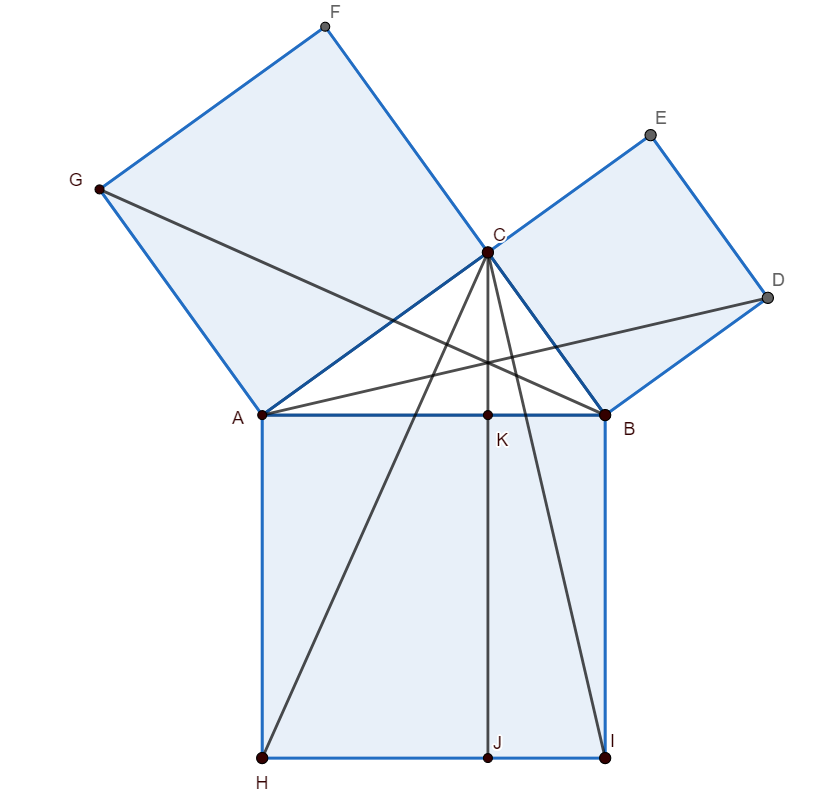
[1] We construct squares BCED on side BC, ABIH on side AB and ACFG on side AC.
[2] Show that the triangles AHC and ABG are congruent.
[3] Now argue that the triangle AGB and the parallelogram ACFG are on the same base and between the same parallels and hence $ar\left( \Delta ABG \right)=\dfrac{1}{2}A{{C}^{2}}$.
[4] Argue that the parallelogram AKJH and the triangle ACH are on the same base and between the same parallels and hence $ar\left( \Delta ACH \right)=\dfrac{1}{2}ar\left( AKJH \right)$
[5] Hence claim that $ar\left( AKJH \right)=A{{C}^{2}}$. With a similar argument claim that $ar\left( BKJI \right)=B{{C}^{2}}$.
[6] Hence prove the Pythagora’s theorem.

Complete step by step answer:
Given: ABC is a right-angled triangle right angled at C.
To prove: $A{{C}^{2}}+B{{C}^{2}}=A{{B}^{2}}$
Construction: Construct square CBDE on side CB, square ACFG on side AC and square ABIH on side AB. Draw CK perpendicular to AB and let it meet on extension with HI at point J. Join CH, CI, BG, and AD.
Proof:
We have $\angle HAC=\angle HAB+\angle BAC$
Since ABIH is a square, we have $\angle HAB=90{}^\circ $
Hence, we have
$\angle HAC=90{}^\circ +\angle BAC$
Again, we have $\angle BAG=\angle BAC+\angle CAG$
Since ACFG is a square, we have $\angle CAG=90{}^\circ $
Hence, we have
$\angle BAG=90{}^\circ +\angle BAC$
Hence, we have
$\angle HAC=\angle BAG$
Now in triangle AHC and triangle ABG, we have
AH = AB (Sides of the same square)
 $\angle HAC=\angle BAG$ (Proved Above)
AC = AG (Sides of the same square)
Hence, by SAS congruency criterion, we have
$\Delta AHC\cong \Delta ABG$
Since congruent triangles have equal areas, we have
$ar\left( \Delta AHC \right)=ar\left( \Delta ABG \right)\,\text{ }\left( i \right)$
Now, we have
Triangle ABG and square AGFC are on the same base AG and between the same parallels, AG and BF.
Hence, we have
$ar\left( \Delta ABG \right)=\dfrac{1}{2}AGFC=\dfrac{A{{C}^{2}}}{2}\text{ }\left( ii \right)$
Also, we have
Triangle ACH and parallelogram AKJH are on the same base AH and between the same parallels, AH and CJ.
Hence, we have
$ar\left( \Delta AKJH \right)=2ar\left( \Delta ACH \right)\text{ }\left( iii \right)$
From equation (i), equation (ii) and equation (iii), we have
$ar\left( AKJH \right)=2\times \dfrac{A{{C}^{2}}}{2}=A{{C}^{2}}\text{ }\left( iv \right)$
By a similar argument as above, we can prove that
$ar\left( BKIJ \right)=B{{C}^{2}}\text{ }\left( v \right)$
Adding equation (iv) and equation (iv), we get
$ar\left( AKJH \right)+ar\left( BKIJ \right)=A{{C}^{2}}+B{{C}^{2}}$
From the above diagram, we have
$ar\left( AKJH \right)+ar\left( BKIJ \right)=ar\left( ABIH \right)=A{{B}^{2}}$
Hence, we have
$A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}$, which completes the proof.

Note:
[1] There are many rearrangement proofs of Pythagoras’ theorem and various geometrical proofs. Pythagoras’ theorem is probably the theorem of mathematics with most proofs which clearly reflects on its importance in the field of Euclidean geometry. Pythagoras’ theorem is the backbone of analytical geometry and was first proven by Pythagoras of Greece and hence the name.